角度问题
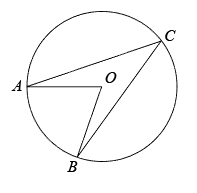
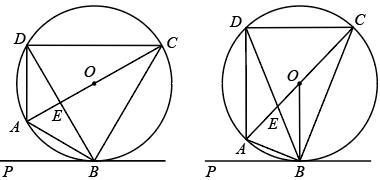
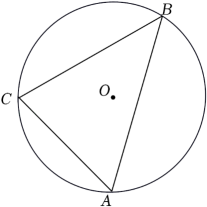
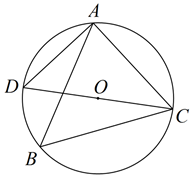
如图,  内接于
内接于  ,CD是
,CD是  的直径,
的直径,  ,则
,则  ( )
( )
- A、 70°
- B、 60°
- C、 50°
- D、 40°
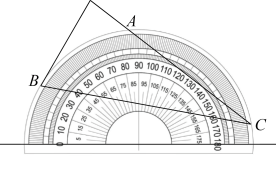
将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
- A、 28°
- B、 30°
- C、 36°
- D、 56°
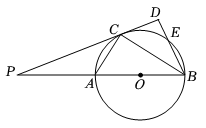
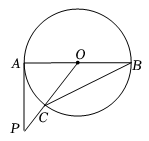
如图,AB是⊙O的直径,PA与⊙O相切于点A,∠ABC=25°,OC的延长线交PA于点P,则∠P的度数是( )
- A、 25°
- B、 35°
- C、 40°
- D、 50°
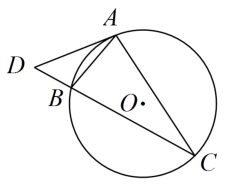
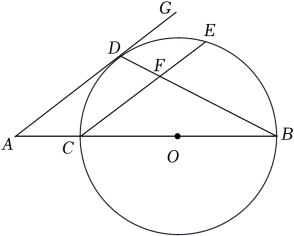
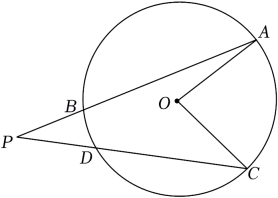
如图,AB,CD是 的弦,延长AB,CD相交于点P.已知
的弦,延长AB,CD相交于点P.已知 ,
,  , 则
, 则 的度数是( )
的度数是( )
- A、 30°
- B、 25°
- C、 20°
- D、 10°
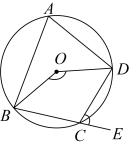
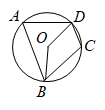
如图,四边形 是
是 的内接四边形.若
的内接四边形.若 , 则
, 则 的度数为( )
的度数为( )
- A、 138°
- B、 121°
- C、 118°
- D、 112°
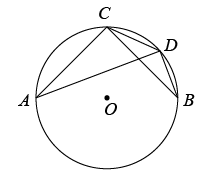
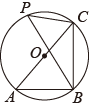
如图,⊙ 是
是 的外接圆,
的外接圆, 是⊙
是⊙ 的直径,点P在⊙
的直径,点P在⊙ 上,若
上,若 , 则
, 则 的度数是( )
的度数是( )
- A、
- B、
- C、
- D、
长度问题
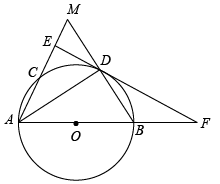
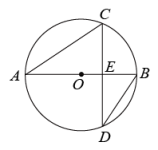
如图, 为
为 的直径,弦
的直径,弦 交
交 于点
于点 ,
,  ,
,  ,
,  , 则
, 则 ( )
( )
- A、
- B、
- C、 1
- D、 2
切线长问题
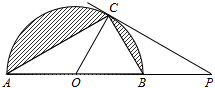
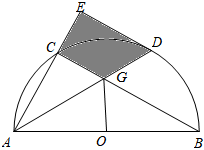
阴影面积问题
圆相关尺规作图
如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说法错误的是( )
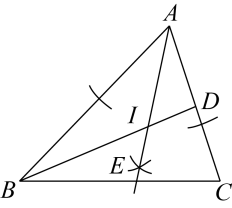
- A、 I到AB,AC边的距离相等
- B、 CI平分∠ACB
- C、 I是△ABC的内心
- D、 I到A,B,C三点的距离相等
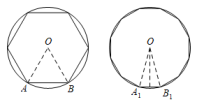
正多边形与圆
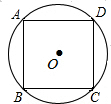
如图,已知 的半径为1,则它的内接正方形
的半径为1,则它的内接正方形 的边长为( )
的边长为( )
- A、
- B、 2
- C、 1
- D、
如图,已知⊙O的周长等于6π,则该圆内接正六边形ABCDEF的边心距OG为( )
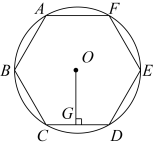
- A、 3
- B、
- C、
- D、 3