2023-2024学年北师大版数学九年级上册4.6利用相似三角形测高（培优卷）

作者UID:12705080

日期: 2024-11-21

同步测试

选择题

一个三角形框架模型的三边长分别为20厘米、30厘米、40厘米，木工要以一根长为60厘米的木条为一边，做一个与模型三角形相似的三角形，那么另两条边的木条长度不符合条件的是（）

A、 30厘米、45厘米；

B、 40厘米、80厘米；

C、 80厘米、120厘米；

D、 90厘米、120厘米

如图，△ABC中，AD⊥BC于D，且有下列条件：（1）∠B＋∠DAC＝90°；（2）∠B＝∠DAC；（3） $\text{[math]}$ ＝ $\text{[math]}$ ；（4）AB²＝BD·BC其中一定能够判定△ABC是直角三角形的共有（　　）

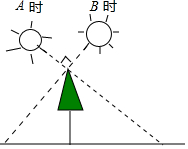
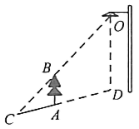
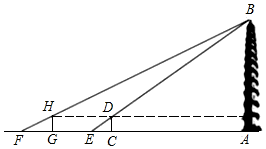
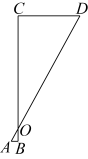
“跳眼法”是炮兵常用的一种简易测距方法，如图，点A为左眼，点B为右眼，点O为右手大拇指，点C为敌人的位置，点D为敌人正左侧方的某一个参照物 $\text{[math]}$ ，已知大多数人的眼距长约为6.4厘米左右，而手臂长约为64厘米左右．若 $\text{[math]}$ 的估测长度为50米，那么 $\text{[math]}$ 的大致距离为（）米．

如图，小红利用小孔成像原理制作了一个成像装置，他在距离纸筒 $\text{[math]}$ 处准备了一支蜡烛，其中纸筒长为 $\text{[math]}$ ，蜡烛长为 $\text{[math]}$ ，则这支蜡烛所成像 $\text{[math]}$ 的高度为（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

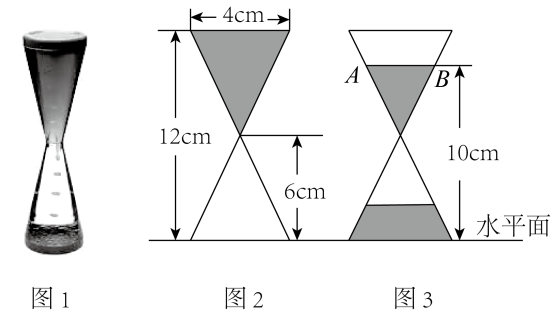
如图，测量小玻璃管口径的量具ABC，AB的长为3cm，AC被分为6等份．若小玻璃管口DE正好对着量具上2等份处（DE∥AB），那么小玻璃管口径DE的长为（）

B、 $\text{[math]}$ cm

D、 $\text{[math]}$ cm

如图，小红利用小孔成像原理制作了一个成像装置，他在距离纸筒 $\text{[math]}$ 处准备了一支蜡烛，蜡烛长为 $\text{[math]}$ ，纸筒的长度为 $\text{[math]}$ ，则这支蜡烛所成像的高度为（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

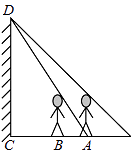
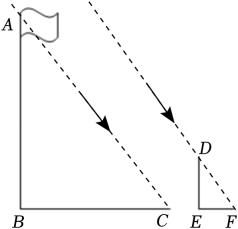
如图，在某一时刻测得1米长的竹竿竖直放置时影长1.2米，在同一时刻旗杆AB的影长不全落在水平地面上，有一部分落在楼房的墙上，他测得落在地面上影长为BD＝9.6米，留在墙上的影长CD＝2米，则旗杆的高度（　　）

如图，A，B两地被池塘隔开，小明通过下列方法测出了A、B间的距离：先在 $\text{[math]}$ 外选一点C，在 $\text{[math]}$ 、 $\text{[math]}$ 上分别找点M，N，使得 $\text{[math]}$ ， $\text{[math]}$ ，测量出 $\text{[math]}$ 的长为 $\text{[math]}$ ，由此可知A、B间的距离为（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

如图，小明在A时测得某树的影长为 $\text{[math]}$ ， B时又测得该树的影长为 $\text{[math]}$ ，若两次日照的光线互相垂直，则树的高度为（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

如图，正方形ABCD中，E为BC的中点，CG⊥DE于G，BG延长交CD于点F，CG延长交BD于点H，交AB于N.下列结论：①DE=CN；② $\text{[math]}$ ；③S_△_DEC=3S_△_BNH；④∠BGN=45°；⑤ $\text{[math]}$ .其中正确结论的个数有（）

填空题

如图，树 $\text{[math]}$ 在路灯O的照射下形成投影 $\text{[math]}$ ，已知路灯高 $\text{[math]}$ ，树影 $\text{[math]}$ ，树 $\text{[math]}$ 与路灯O的水平距离 $\text{[math]}$ ，则树的高度 $\text{[math]}$ 长是 $\text{[math]}$ .

测量附中国旗杆的高度，小宇的测量方法如下：如图，将直角三角形硬纸板△DEF的斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上．测得DE＝0.5米，EF＝0.25米，目测点D到地面的距离DG＝1.6米，到旗杆的水平距离DC＝18米．按此方法，可计算出旗杆的高度为米．

如图，小亮测得学校门口栏杆的短臂 $\text{[math]}$ 长1米，长臂 $\text{[math]}$ 长4米，当短臂外端A下降0.6米时，长臂外端B升高米．

墙壁CD上D处有一盏灯（如图），小明站在A站测得他的影长与身长相等都为1.5m，他向墙壁走1m到B处时发现影子刚好落在A点，则灯泡与地面的距离CD=m.

如图1是液体沙漏的立体图形，图2，图3分别是液体沙漏某一时刻沙漏上半部分液体长度与液面距离水平面高度的平面示意图，则图3中AB＝cm．

解答题

杭州市西湖风景区的雷峰塔又名“皇妃塔”，某校社会实践小组为了测量雷峰塔的高度，在地面上C处垂直于地面竖立了高度为2米的标杆 $\text{[math]}$ ，这时地面上的点E，标杆的顶端点D，雷峰塔的塔尖点B正好在同一直线上，测得 $\text{[math]}$ 米，将标杆 $\text{[math]}$ 向后平移到点G处，这时地面上的点F，标杆的顶端点H，雷峰塔的塔尖点B正好又在同一直线上（点F，点G，点E，点C与塔底处的点A在同一直线上），这时测得 $\text{[math]}$ 米， $\text{[math]}$ 米，请你根据以上数据，计算雷峰塔的高度 $\text{[math]}$ .

如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图，在点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，CD⊥BD，且测得AB＝4m，BP＝6m，PD＝12m，求该古城墙CD的高度是多少m？

5月10日上午，庆祝中国共产主义青年团成立100周年大会在北京人民大会堂隆重举行，习近平总书记重要讲话引发各界青年热烈反响．某校为庆祝共青团成立100周年升起了共青团旗帜，李优和贺基旭想用所学知识测量该旗帜的宽度MN，他们进行了如下操作：如图，首先，李优在C处竖立一根标杆 $\text{[math]}$ ，地面上的点A、标杆顶端B和点N在一条直线上， $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米；然后，贺基旭手持自制直角三角纸板 $\text{[math]}$ ，使长直角边 $\text{[math]}$ 与水平地面平行，调整位置，恰好在P点时点D、E、M在一条直线上， $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点P、G、C、A在同一水平直线上，点N在 $\text{[math]}$ 上，求旗帜的宽度 $\text{[math]}$ ．

如图，某数学学习小组为了测量直立在水平地面上的旗杆AB的高度，把标杆DE直立在同一水平地面上，同一时刻测得旗杆和标杆在太阳光下的影长分别BC＝9.6m，EF＝2.4m.已知B，C，E，F点在同一直线上，且AB⊥BC，DE⊥EF，DE＝3.1m，求旗杆AB的高度.

用一个大小形状固定的不等边锐角三角形纸，剪出一个最大的正方形纸备用.甲同学说：“当正方形的一边在最长边时，剪出的内接正方形最大”；乙同学说：“当正方形的一边在最短边上时，剪出的内接正方形最大”；丙同学说：“不确定，剪不出这样的正方形纸.”你认为谁说的有道理，请证明.（假设图中△ABC的三边a，b，c，且a＞b＞c，三边上的高分别记为h_a ， h_b ， h_c）

试卷列表

教育网站链接

在线组卷课件下载评课网课件工坊 PPT模板排课软件云字帖