阅读材料:怎样证实“两直线平行,同位角相等”
本节中,我们用叠合的方法发现了“两直线平行,同位角相等” .事实上,这个结论可以运用已有的基本事实,通过说理加以证实.
如图,直线AB、CD被直线EF所截,AB//CD,∠1与∠2是同位角.
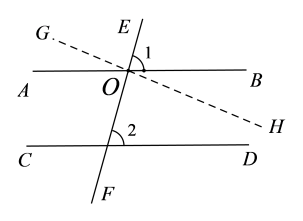
假设∠1 ∠2,那么可以通过直线AB与EF的交点O作直线GH,使∠EOH=∠2,直线GH与直线AB是两条直线.
∠2,那么可以通过直线AB与EF的交点O作直线GH,使∠EOH=∠2,直线GH与直线AB是两条直线.
根据基本事实“同位角相等,两直线平行”,由∠EOH=∠2,可以得到GH//CD.
这样,过点O就有两条直线AB、GH都与CD平行.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”矛盾.
这说明∠1 ∠2的假设不正确,于是∠1=∠2.
∠2的假设不正确,于是∠1=∠2.
解决问题:若 且
且 , 请你用以上方法说明:
, 请你用以上方法说明: .
.