选择题
在一个不透明的盒子中,红色、白色、黑色的球共有40个,除颜色外其他完全相同,老师在课堂上组织同学通过多次试验后发现其中摸到红色、白色的频率基本稳定在45%和15%,则盒子中黑色球的个数可能是( ).
- A、 16
- B、 18
- C、 20
- D、 22
一个口袋中有红球、黄球共20个,这些除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一球,记下颜色后再放回口袋,不断重复这一过程,共摸了200次,发现其中有161次摸到红球.则这个口袋中红球数大约有( )
- A、 4个
- B、 10个
- C、 16个
- D、 20个
随机抛掷一枚瓶盖1000次,经过统计得到“正面朝上”的次数为420次,则可以由此估计抛掷这枚瓶盖出现“反面朝上”的概率为( )
- A、 0.22
- B、 0.42
- C、 0.50
- D、 0.58
在一个不透明的口袋中,装有除颜色外其他都相同的4个白球和n个黄球,某同学进行如下试验:从袋中随机摸出1个球记下它的颜色,放回、摇匀,为一次摸球试验,记录摸球的次数与摸出白球的次数的列表如下:
摸球试验的次数 | 100 | 200 | 500 | 1000 |
摸出白球的次数 | 21 | 39 | 102 | 199 |
根据列表可以估计出n的值为( )
- A、 16
- B、 4
- C、 20
- D、 24
如图,在由大小相同的小正方形组成的网格中有一条“心形线”.数学小组为了探究随机投放一个点恰好落在“心形线”内部的概率,进行了计算机模拟试验,得到如下数据:
试验总次数 | 100 | 200 | 300 | 500 | 1500 | 2000 | 3000 |
落在“心形线”内部的次数 | 61 | 93 | 165 | 246 | 759 | 996 | 1503 |
落在“心形线”内部的频率 | 0.610 | 0.465 | 0.550 | 0.492 | 0.506 | 0.498 | 0.501 |
根据表中的数据,估计随机投放一点落在“心形线”内部的概率为( )

- A、 0.46
- B、 0.50
- C、 0.55
- D、 0.61
某小组做“当试验次数很大时,用频率估计概率”的试验时,统计了某一结果出现的频率,表格如下,则符合这一结果的试验最有可能是( )
次数 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
频率 | 0.60 | 0.30 | 0.50 | 0.36 | 0.42 | 0.38 | 0.41 | 0.39 | 0.40 | 0.40 |
- A、 掷一个质地均匀的骰子,向上的面点数是“6”
- B、 掷一枚一元的硬币,正面朝上
- C、 不透明的袋子里有2个红球和3个黄球,除颜色外都相同,从中任取一球是红球
- D、 三张扑克牌,分别是3,5,5,背面朝上洗匀后,随机抽出一张是5
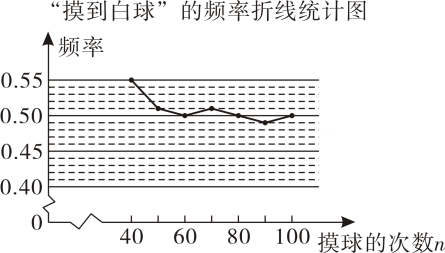
某学习小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如下折线统计图,则符合这一结果的试验最有可能的是( )

- A、 先后两次掷一枚之地均匀的硬币,一次正面朝上一次反面朝上
- B、 先后两次掷一枚之地均匀的硬币,两次都出现反面朝上
- C、 掷一枚之地均匀的正六面体骰子,向上面的点数是偶数
- D、 掷一枚之地均匀的正六面体骰子,向上面的点数是2或4