选择题
4的算术平方根是( )
- A、 2
- B、 ﹣2
- C、 ±2
- D、
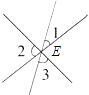
如图,三条直线l1 , l2 , l3相交于点E,则∠1+∠2+∠3=( )
- A、 90°
- B、 120°
- C、 180°
- D、 360°
在实数0、n、  、
、  、﹣
、﹣  中,无理数的个数有( )
中,无理数的个数有( )
- A、 1个
- B、 2个
- C、 3个
- D、 4个
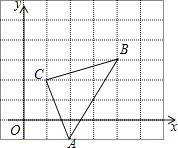
如图,已知棋子“车”的坐标为(﹣2,﹣1),棋子“马”的坐标为(1,﹣1),则棋子“炮”的坐标为( )
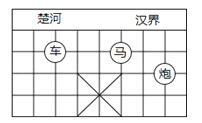
- A、 (3,2)
- B、 (﹣3,2)
- C、 (3,﹣2)
- D、 (﹣3,﹣2)
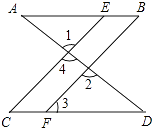
如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( )
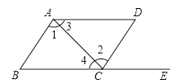
- A、 ∠3=∠4
- B、 ∠1=∠2
- C、 ∠B=∠DCE
- D、 ∠D+∠DAB=180°
有下列三个命题:
(1)两点之间线段最短
(2)平面内,过一点能且只能作一条直线与已知直线垂直
(3)过直线外一点有且只有一条直线与这条直线平行
其中真命题的个数是( )
- A、 0个
- B、 1个
- C、 2个
- D、 3个
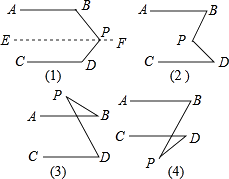
若点A(2,﹣2),B(﹣1,﹣2),则直线AB与x轴和y轴的位置关系分别是( )
- A、 相交,相交
- B、 平行,平行
- C、 平行,垂直相交
- D、 垂直相交,平行
已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标为( )
- A、 (﹣4,0)
- B、 (6,0)
- C、 (﹣4,0)或(6,0)
- D、 无法确定
同一平面内,三条不同直线的交点个数可能是( )个.
- A、 1或3
- B、 0、1或3
- C、 0、1或2
- D、 0、1、2或3
如图,直径为1个单位长度的圆从A点沿数轴向右滚动(无滑动)两周到达点B,则点B表示的数是( )
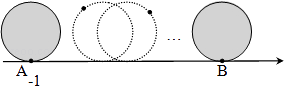
- A、 π
- B、 2π
- C、 2π﹣1
- D、 2π+1.