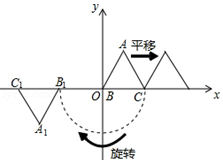
定义：在平面直角坐标系中，一个图形先向右平移a个单位，再绕原点按顺时针方向旋转θ角度，这样的图形运动叫作图形的γ（a，θ）变换．如图，等边△ABC的边长为1，点A在第一象限，点B与原点O重合，点C在x轴的正半轴上．△A₁B₁C₁就是△ABC经γ（1，180°）变换后所得的图形．若△ABC经γ（1，180°）变换后得△A₁B₁C₁ ， △A₁B₁C₁经γ（2，180°）变换后得△A₂B₂C₂ ， △A₂B₂C₂经γ（3，180°）变换后得△A₃B₃C₃ ， 依此类推……△A_n﹣1B_n﹣1C_n﹣1经γ（n，180°）变换后得△A_nB_nC_n ， 则点A₁的坐标是，点A₂₀₂₀的坐标是．