填写下列空格

已知：如图，点E在BC上，BD⊥AC，EF⊥AC，垂足分别为D、F，点M、G在AB上，

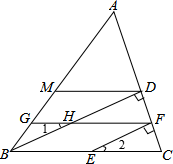
∠AMD=∠AGF，∠1=∠2．

求证：DM∥BC

证明：∵BD⊥AC，EF⊥AC，垂足分别为D、F（已知）

∴∠BDC=90°，∠EFC=90°（垂直的定义）

∴∠BDC=∠EFC（等量代换）

∴（同位角相等，两直线平行）

∠2=∠CBD（）

∠1=∠2（已知）

∠1=∠CBD（）

∴（）

∴∠AMD=∠AGF（已知）

∴DM∥GF（同位角相等，两直线平行）

∴DM∥BC（）