阅读以下材料，并按要求完成相应的任务：

莱昂哈德·欧拉（LeonhardEuler）是瑞士数学家，在数学上经常见到以他的名字命名的重要常数、公式和定理，下面是欧拉发现的一个定理：在△ABC中，R和r分别为外接圆和内切圆的半径，O和I分别为其外心和内心，则OI =R -2Rr.

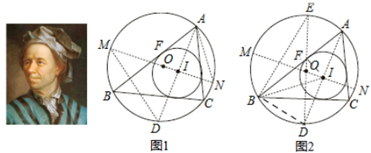
下面是该定理的证明过程（借助了第（2）问的结论）：

延长AI交⊙O于点D，过点I作⊙O的直径MN，连接DM，AN.

∵∠D=∠N，∴∠DMI=∠NAI（同弧所对的圆周角相等），

∴△MDI∽△ANI.∴ ，∴IA×ID=IM×IN①

如图②，在图1（隐去MD，AN）的基础上作⊙O的直径DE，连接BE，BD，BI，IF

∵DE是⊙O的直径，∴∠DBE=90°.

∵⊙I与AB相切于点F，∴∠AFI=90°，

∴∠DBE=∠IFA．

∵∠BAD=∠E（同弧所对圆周角相等），

∴△AIF∽△EDB．

∴ ，∴ ②，

由（2）知： ，

∴

又∵ ，

∴2Rr=（R+d）（R-d），

∴R -d =2Rr

∴d =R -2Rr

任务：