阅读下面解答过程，并填空或在括号内填写理由．

已知BE平分∠ABC交AC于点E，DE∥BC，且∠ABC＝110°，∠C＝35°，

请说明BE⊥AC．

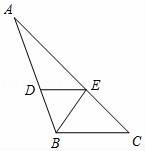
解：∵BE平分∠ABC（已知），

∴∠EBC＝ ∠（角平分线定义）．

∵∠ABC＝110°，

∴∠EBC＝°．

∵DE∥BC，∠C＝35°（已知），

∴∠EBC＝∠（两直线平行，内错角相等），

∠C＝∠AED＝35°（）．

∴∠AEB＝∠+∠＝90°．

∴BE⊥AC．