如图1，在△ABC中，设∠A、∠B、∠C的对边分别为a，b，c，过点A作AD⊥BC，垂足为D，会有sin∠C=，【参考答案】

试题详情

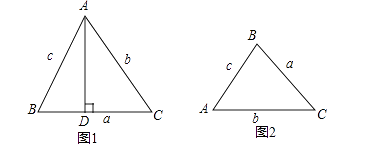
如图1，在△ABC中，设∠A、∠B、∠C的对边分别为a，b，c，过点A作AD⊥BC，垂足为D，会有sin∠C= $\text{[math]}$ ，则

S_△_ABC= $\text{[math]}$ BC×AD= $\text{[math]}$ ×BC×ACsin∠C= $\text{[math]}$ absin∠C，

即S_△_ABC= $\text{[math]}$ absin∠C

同理S_△_ABC= $\text{[math]}$ bcsin∠A

S_△_ABC= $\text{[math]}$ acsin∠B

通过推理还可以得到另一个表达三角形边角关系的定理﹣余弦定理：

如图2，在△ABC中，若∠A、∠B、∠C的对边分别为a，b，c，则

a²=b²+c²﹣2bccos∠A

b²=a²+c²﹣2accos∠B

c²=a²+b²﹣2abcos∠C

用上面的三角形面积公式和余弦定理解决问题：

知识点

参考答案