古希腊有一个著名的“将军饮马问题”，大致内容如下：古希腊一位将军，每天都要巡查河岸同侧的两个军营A，B． 他总是先去A营，再到河边饮马，之后，再巡查B营．他时常想，怎么走，才能使他每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题．

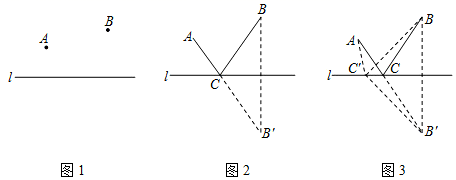
如图2，作B关于直线l的对称点B′，连结AB′与直线l交于点C， 点C就是所求的位置．

证明：如图3，在直线l上另取任一点C′，连结AC′，BC，B′C′，

∵直线l是点B，B′的对称轴，点C，C′在l上，

∴CB=   ▲  ，C′B=   ▲  ，

∴AC+CB=AC+CB′=   ▲  ．

在△AC′B′，

∵AB′＜AC′+C′B′，

∴AC+CB＜AC′+C′B′即AC+CB最小．

本问题实际上是利用轴对称变换的思想，把A，B在直线同侧的问题转化为在直线的两侧，从而可利用“两点之间线段最短”，即“三角形两边之和大于第三边”的问题加以解决（其中C在AB′与l的交点上，即A，C，B′三点共线）．本问题可归纳为“求定直线上一动点与直线外两定点的距离和的最小值”的问题的数学模型．

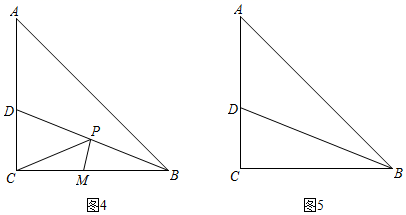
拓展应用：如图，等腰直角△ABC中，∠ACB= 90°，BD平分∠ABC交AC于D， 点P是BD上一个动点，点M是BC上一个动点，请在图5中画出PC+PM的值最小时P的位置．（可用三角尺）