在学习矩形的过程中，小明遇到了一个问题：在矩形ABCD中，E是AD边上的一点，试说明△BCE的面积与矩形ABCD的面积之间的关系．他的思路是：首先过点E作BC的垂线，将其转化为证明三角形全等，然后根据全等三角形的面积相等使问题得到解决．请根据小明的思路完成下面的作图与填空：证明：用直尺和圆规，过点E作BC的垂线EF，垂足为F(只保留作图痕迹).

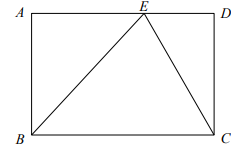
在△BAE和△EFB中，

∵EF⊥BC，

∴∠EFB=90°.

又∠A=90°，

∴▲①

∵AD∥BC，

∴▲②

又▲③

∴△BAE≌△EFB(AAS)．

同理可得▲④