问题提出：如图是某城市规划的“五横五纵”轨道交通示意图（每条线的交点代表一个站点），如果要想从站点A到站点B（只能按照从上往下，从左往右的方向行进），那么会有多少种不同的线路可以选择？

问题探究：为了解决问题，我们可以采用从特殊到一般的数学思想，先从最简单的情形入手，从中找到解决问题的方法．

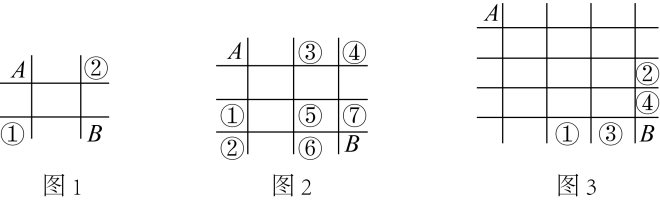探究一：如果有“两横两纵”四条轨道，如图1所示要想从站点A到达站点B，要么先从上往下到站点①，要么先从左往右到站点②，而从站点A到达站点①，站点②的路线都只有一条，所以，从站点A到达站点B的路线数为到达站点①和站点②的路线数之和，即1＋1＝2条．

探究二：如果有“三横三纵”六条轨道，如图2所示．要想从站点A到达站点B，必须先到达站点⑥或者站点⑦，所以为了探究从站点A到达站点B的路线数，我们可以先探究从站点A到达站点⑥和站点⑦的路线数，两者之和即为从站点A到达站点B的路线数．由探究一可知，从站点A到达站点⑤，有1＋1＝2条路线，从站点A直接到达站点②，只有1条路线，所以，从站点A到达站点⑥共有1＋2＝3条路线；从站点A直接到达站点④，也只有1条路线，所以，从站点A到达站点⑦共有1＋2＝3条路线，因此，从站点A到达站点B共有3＋3＝6条路线．

探究三：如果有“四横四纵”八条轨道，如图3所示．要想从站点A到达站点B，请仿照上面的探究过程，完成下表：

站点	①	②	③	④	B
路线数