根据以下素材，完成探索任务.

问题的提出

根据以下提供的素材，在总费用（新墙的建筑费用与门的价格和）不高于6400元的情况下，如何设计最大饲养室面积的方案？

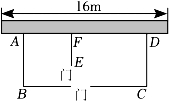
素材1：图1是某农场拟建两间矩形饲养室，饲养室的一面靠现有墙，中间用一道墙隔开，计划中建筑材料可建围墙的总长为20m，开2个门，且门宽均为1m.

素材2：2个门要求同一型号，有关门的采购信息如表.

如表

型号	A	B	C
规格（门宽）	1米	1.2米	1米
单价（元）	250	280	300

素材3：与现有墙平行方向的墙建筑费用为400元/米，与现有墙垂直方向的墙建筑费用为200元/米.

问题解决

任务1	确定饲养室的形状 设AB＝x，矩形ABCD的面积为S，求S关于x的函数表达式.
任务2	探究自变量x的取值范围.
任务3	确定设计方案 我的设计方案是选型号▲门，AB＝▲m，BC＝▲m，S的最大值为▲m2.