学完平移与旋转后，数学老师再次介绍了截长补短法：截长补短法是初中几何题中一种添加辅助线的方法，也是把几何题化难为易的一种策略．截长就是在长边上截取一条线段与某一短边相等，补短就是通过延长或者旋转等方式使两条短边拼合到一起，从而解决问题．

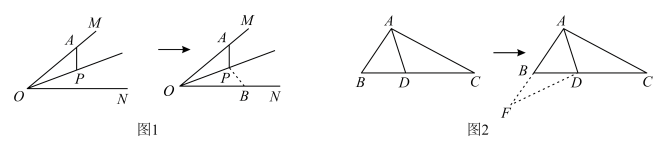
例如：如图1，已知点P是的平分线上一点，点A是射线上任意一点，在上截取B点，使（截长法），连接 ， 易得： ． 如图2，已知中，平分 ， 延长至点F（补短法），使得 ， 连接 ， 易得 ．

问题情境：

今天我们继续运用截长补短法进行探究学习．如图3，点P是等边外一点，连接且满足 ， 线段之间有何等量关系呢？

经过探究，勤奋小组讲解了他们的思路：

如图4，在上截取一点Q，使 ， 连接 ．

∵是等边三角形， 

∴ ，

又∵ ， ∴ ，

又∵ ∴

∴（依据1：    ▲        ）

∴ ，

∴ ， 即

可知是等边三角形（依据2：    ▲        ），所以 ， 因此最终得出线段 之间的等量关系是    ▲         ．