请根据素材，完成任务.素材一如图，在Rt中，，垂足为点，若保证始终为直角，则点A、B、C在以AB为直径的【参考答案】

试题详情

请根据素材，完成任务.

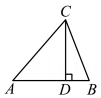
素材一	如图，在Rt $\text{[math]}$ 中， $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，若保证 $\text{[math]}$ 始终为直角，则点A、B、C在以AB为直径的圆上.
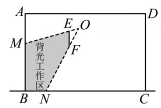
素材二	如图，在Rt△ABC中， $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，取AB的中点 $\text{[math]}$ ，连接OC，根据“直角三角形斜边上的中线等于斜边的一半”可知 $\text{[math]}$ ，可得OC≥CD.
素材三	如图，矩形ABCD是某实验室侧截面示意图，现需要在室内安装一块长1米的遮光板EF，且EF//AB，点 $\text{[math]}$ 到墙AB的距离为4米，到地面BC的距离为5米.点O为室内光源，OM、ON为光线， $\text{[math]}$ ，通过调节光源的位置，可以改变背光工作区的大小.若背光工作区BM+BN的和最大时，该实验室“可利用比”最高.
任务一	若素材一中的AB=4，求CD的最大值.
任务二	若素材二中的CD=6，求AB的最小值.
任务三	若任务二中的∠ACB=90°改成∠ACB=60°，其余条件不变，请直接写出AB的最小值.
任务四	若任务二中的∠ACB=90°，CD=6改成∠ACB=α，CD=m，请直接出AB的最小值.
任务五	当素材三中的实验室“可利用比”最高，求此时BM+BN的值

知识点

参考答案