选择题
已知全集U={1,2,3,4,5},A={1,3},则  ( )
( )
- A、
- B、 {1,3}
- C、 {2,4,5}
- D、 {1,2,3,4,5}
双曲线  的焦点坐标是( )
的焦点坐标是( )
- A、 (−
,0),(
,0)
- B、 (−2,0),(2,0)
- C、 (0,−
),(0,
)
- D、 (0,−2),(0,2)
某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )

- A、 2
- B、 4
- C、 6
- D、 8
复数  (i为虚数单位)的共轭复数是( )
(i为虚数单位)的共轭复数是( )
- A、 1+i
- B、 1−i
- C、 −1+i
- D、 −1−i
函数y=  sin2x的图象可能是( )
sin2x的图象可能是( )
- A、
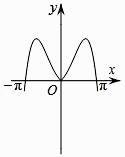
- B、
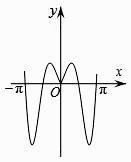
- C、
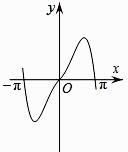
- D、

已知平面α, 直线m,n满足m α,n
α,n α, 则“m∥n”是“m∥α”的( )
α, 则“m∥n”是“m∥α”的( )
- A、 充分不必要条件
- B、 必要不充分条件
- C、 充分必要条件
- D、 既不充分也不必要条件
设0<p<1,随机变量ξ的分布列是
ξ | 0 | 1 | 2 |
P |
则当p在(0,1)内增大时,( )
- A、D(ξ)减小
- B、D(ξ)增大
- C、D(ξ)先减小后增大
- D、D(ξ)先增大后减小
已知四棱锥S−ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成的角为θ1 ,SE与平面ABCD所成的角为θ2 , 二面角S−AB−C的平面角为θ3 , 则( )
- A、θ1≤θ2≤θ3
- B、θ3≤θ2≤θ1
- C、θ1≤θ3≤θ2
- D、θ2≤θ3≤θ1
已知a,b,e是平面向量,e是单位向量.若非零向量a与e的夹角为  ,向量b满足b2−4e·b+3=0,则|a−b|的最小值是( )
,向量b满足b2−4e·b+3=0,则|a−b|的最小值是( )
- A、
−1
- B、
+1
- C、 2
- D、 2−
已知  成等比数列,且
成等比数列,且  .若
.若  ,则( )
,则( )
- A、
- B、
- C、
- D、

