单选题
下列四个数中,其绝对值小于2的数是( )
- A、
- B、
- C、
- D、 ﹣3
截至5月5日中午,2021年五一档总票房(含预售)突破15.27亿,观影总人次4034.22万,总场次225.31万,打破了五一档票房、人次、场次三项影视记录,15.27亿用科学记数法表示为( )
- A、
- B、
- C、
- D、
一个口袋中有3个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,再放回,不断重复上述过程.小明共摸了100次,其中80次摸到白球.根据上述数据,小明可估计口袋中的白球大约有( )
- A、 18个
- B、 15个
- C、 12个
- D、 10个
下列用数轴表示不等式组  的解集中,正确的是( )
的解集中,正确的是( )
- A、

- B、

- C、

- D、

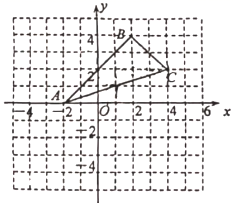
如图,二次函数  的图象与反比例函数
的图象与反比例函数  的图象交于
的图象交于  三点.若
三点.若  ,则x的取值范围是( )
,则x的取值范围是( )

- A、
- B、
或
- C、
或
- D、
或