单选题
方程  的根是( )
的根是( )
- A、
- B、
- C、
- D、
一元二次方程x(x﹣2)=x﹣2的根是( )
- A、x=2
- B、x1=0,x2=2
- C、x1=2,x2=1
- D、x=﹣1
方程  的解是( )
的解是( )
- A、 2或0
- B、 ±2或0
- C、 2
- D、 -2或0
已知直角三角形的两条边长分别是方程x2-14x+48=0的两个根,则此三角形的第三边是( )
- A、 6或8
- B、 10或
- C、 10或8
- D、
方程  的解为( )
的解为( )
- A、
- B、
- C、
,
- D、
,
已知实数x满足(x2﹣2x+1)2+4 (x2﹣2x+1)﹣5=0,那么x2﹣2x+1的值为( )
- A、 ﹣5或1
- B、 ﹣1或5
- C、 1
- D、 5
方程2x(x﹣3)=5(x﹣3)的根是( )
- A、 x=
- B、 x=3
- C、 x1=
,x2=3
- D、 x1=﹣
,x2=3
下列说法中,正确的说法有( )
①对角线互相平分且相等的四边形是菱形;
②一元二次方程 的根是
,
;
③两个相似三角形的周长的比为 ,则它们的面积的比为
;
④对角线互相垂直的平行四边形为正方形;
⑤对角线垂直的四边形各边中点得到的四边形是矩形.
- A、 1个
- B、 2个
- C、 3个
- D、 4个
已知关于x的一元二次方程3x2﹣2xy-y2=0的,则  ( )
( )
- A、 1
- B、 1或
- C、 1或﹣
- D、 ﹣
如图,在平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x﹣3=0的根,则平行四边形ABCD的周长为( )
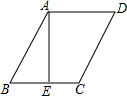
- A、 12-6
- B、 6
+12
- C、 4+2
- D、 4-2