选择题(每小题2分,共12分)
以下四家银行的行标图中,是轴对称图形的有( )

- A、 1个
- B、 2个
- C、 3个
- D、 4个
下列运算正确的是( )
- A、 (a+b)2=a2+b2
- B、 (﹣2a2b)3=﹣8a5b3
- C、 a6÷a3=a2
- D、 a3•a2=a5
石墨烯(Graphene)是人类已知强度最高的物质,据科学家们测算,要施加55牛顿的压力才能使0.000001米长的石墨烯断裂,其中0.000001用科学记数法表示为( )
- A、 1×10﹣6
- B、 10×10﹣7
- C、 0.1×10﹣5
- D、 1×106
下列约分正确的是( )
- A、
=
- B、
=x3
- C、
- D、
=
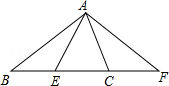
如图,AE、AD分别是△ABC的高和角平分线,∠B=36°,∠C=76°,则∠DAE的度数为( )

- A、 40°
- B、 20°
- C、 18°
- D、 38°