单选题
下面运算结果为 的是
的是

- A、
- B、
- C、
- D、
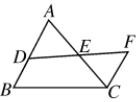
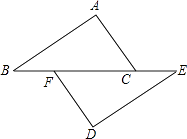
如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
- A、 AB=DE
- B、 AC=DF
- C、 ∠A=∠D
- D、 BF=EC
下列式子:①  ,②
,②  ,③
,③  ,④
,④  ,其中是分式的有( )
,其中是分式的有( )
- A、 1个
- B、 2个
- C、 3个
- D、 4个
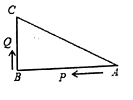
若直角三角形的三边长为6,8,m,则m2的值为( )
- A、 10
- B、 100
- C、 28
- D、 100或28
下列因式分解正确的是( )
- A、
- B、
- C、
- D、
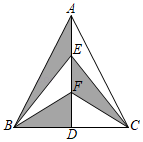
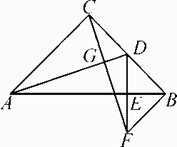
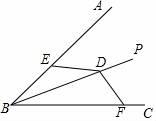
如图,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE=DF,若∠BED=140°,则∠BFD的度数是( )
- A、 40°
- B、 50°
- C、 60°
- D、 70°
与  可以合并的二次根式是( )
可以合并的二次根式是( )
- A、
- B、
- C、
- D、
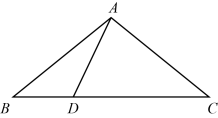
如图,在 中,
中, ,
,  ,
,  是线段
是线段 上的动点(不含端点
上的动点(不含端点 、
、 ).若线段
).若线段 长为正整数,则点
长为正整数,则点 的个数共有( )
的个数共有( )
- A、 4个
- B、 3个
- C、 2个
- D、 1个
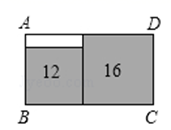
如图,在长方形  中无重叠放入面积分别为
中无重叠放入面积分别为  和
和  的两张正方形纸片,则图中空白部分的面积为( )
的两张正方形纸片,则图中空白部分的面积为( ) 
- A、
- B、
- C、
- D、
若关于x的分式方程 无解,则m的值为( )
无解,则m的值为( )
- A、 0
- B、 2
- C、 0或2
- D、 ±2