单选题
一列数1,3,7,13,…,按此规律排列,第6个数是( )
- A、 21
- B、 31
- C、 43
- D、 57
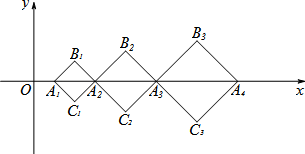
正方形ABCD在数轴上的位置如图所示,点D,A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2019次后,数轴上数2019所对应的点是( )

- A、 点C
- B、 点D
- C、 点A
- D、 点B
某人的身份证号码是320922199904010012,此人的生日是( )
- A、 9月4日
- B、 10月1日
- C、 4月1日
- D、 9月22日
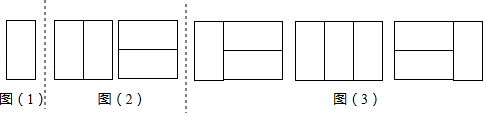
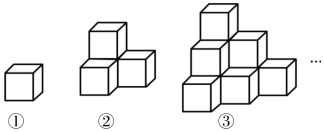
观察下列图形,图(1)中有3个三角形,图(2)中有5个三角形,图(3)中有7个三角形,…若依此规律下去,则第5个图形中三角形的个数是( )

- A、 9个
- B、 11个
- C、 13个
- D、 15个
我国是最早认识负数,并进行相关运算的国家在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算  的过程按照这种方法,图2表示的过程应是在计算( )
的过程按照这种方法,图2表示的过程应是在计算( )

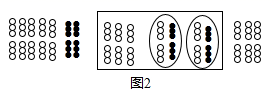
- A、
- B、
- C、 5+2
- D、
如图,小明用棋子摆了几个“开”字,其中第①个“开”字用了14个棋子,第②个“开”字用了20个棋子,第③个“开”字用了26个棋子…,照此规律继续摆下去,第7个图需用到的棋子数为( )
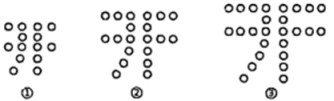
- A、 38
- B、 44
- C、 50
- D、 56
如图,直线  与
与  轴、
轴、  轴分别相交于点A、B,过点B作
轴分别相交于点A、B,过点B作  ,使
,使  .将
.将  绕点
绕点  顺时针旋转,每次旋转
顺时针旋转,每次旋转  .则第2022次旋转结束时,点
.则第2022次旋转结束时,点  的对应点
的对应点  落在反比例函数
落在反比例函数  的图象上,则
的图象上,则  的值为
的值为 


- A、 -4
- B、 4
- C、 -6
- D、 6
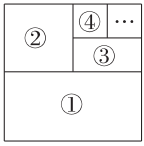
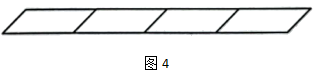
如图,宽为30 cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的长为( )

- A、 10 cm
- B、 18 cm
- C、 20 cm
- D、 24 cm
如图是用灰白两种颜色的纸片按一定的规律摆成的图案,依此规律继续摆下去,若第n个图案中白色纸片的个数是1564,则n的值为( )

- A、 520
- B、 521
- C、 523
- D、 524
现有一列式子:①  ;②
;②  ;③
;③  ,则第⑧个式子的计算结果用科学记数法可表示为( )
,则第⑧个式子的计算结果用科学记数法可表示为( )
- A、
- B、
- C、
- D、
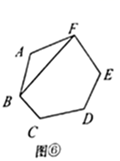
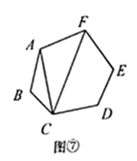
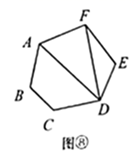
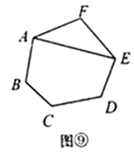
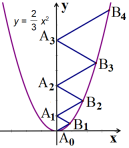
如图,在平面直角坐标系中,将等边  绕点A旋转180°,得到
绕点A旋转180°,得到  ,再将
,再将  绕点
绕点  旋转180°,得到
旋转180°,得到  ,再将
,再将  绕点
绕点  旋转180°,得到
旋转180°,得到  ,…,按此规律进行下去,若点
,…,按此规律进行下去,若点  ,则点
,则点  的坐标为( )
的坐标为( )

- A、
- B、
- C、
- D、
将数按以下规律排列:1,2,3,2,5,2,7,2,9,2,11……,以此类推,四个同学分别得出一个结论:
杨一:第99个数是99;
张三:第2022个数是2;
李四:前101个数的和为2652;
王五,前200个数中有7个完全平方数;
四个结论正确的有( )个
- A、 4
- B、 3
- C、 2
- D、 1
如图,各正方形中的四个数之间都有相同的规律,根据此规律,x的值为( )

- A、 242
- B、 232
- C、 220
- D、 252
如图,分别用火柴棍连续搭建等边三角形和正六边形,公共边只用一根火柴棍.如果搭建等边三角形和正六边形共用了2018根火柴,并且等边三角形的个数比正六边形的个数多7,那么连续搭建的等边三角形的个数是( )

- A、 291
- B、 292
- C、 293
- D、 294
已知整数 、
、 、
、 、
、 、……满足下列条件:
、……满足下列条件: ,
,  ,
,  ,
,  , …,
, …, (n为正整数)依此类推,则
(n为正整数)依此类推,则 的值为( )
的值为( )
- A、 -1010
- B、 -2020
- C、 -1011
- D、 -2022
如图所示,直线 相交于点
相交于点 , “阿基米德曲线”从点
, “阿基米德曲线”从点 开始生成,如果将该曲线与每条射线的交点依次标记为
开始生成,如果将该曲线与每条射线的交点依次标记为 ….那么标记为“
….那么标记为“ ”的点在( )
”的点在( )

- A、 射线
上
- B、 射线
上
- C、 射线
上
- D、 射线
上









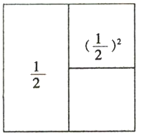 ⇒
⇒ 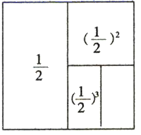 ⇒
⇒ 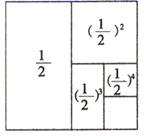 ⇒
⇒