第六题
分式方程 的解是( )
的解是( )
- A、 x=2
- B、 x=4
- C、 x=6
- D、 x=8
若关于x的方程 的解为正数,则m的取值范围为( )
的解为正数,则m的取值范围为( )
- A、
- B、
且
- C、
- D、
且
已知关于 的分式方程
的分式方程 的解为负数,则
的解为负数,则 的取值范围是( )
的取值范围是( )
- A、
- B、
且
- C、
且
- D、
设m,n为实数,定义如下一种新运算:m☆n =  ,若关于x的方程a(x☆x)=(x☆12)+1无解 ,则a的值是( )
,若关于x的方程a(x☆x)=(x☆12)+1无解 ,则a的值是( )
- A、 4
- B、 ﹣3
- C、 4或﹣3
- D、 4或3
若整数a使关于x的不等式组  无解,且使关于x的分式方程
无解,且使关于x的分式方程  有整数解,那么所有满足条件的a的值的积是( )
有整数解,那么所有满足条件的a的值的积是( )
- A、 2
- B、 3
- C、
- D、 8
已知公式  (
(  ),则表示
),则表示  的公式是( )
的公式是( )
- A、
- B、
- C、
- D、
第七题
某体育比赛的门票分A票和B票两种,A票每张x元,B票每张y元.已知10张A票的总价与19张B票的总价相差320元,则( )
- A、
- B、
- C、 |10x-19y|=320
- D、 |19x-10y|=320
相同规格(长为14,宽为8)的长方形硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,有如图所示的甲、乙两种方案,所得长方体体积分别记为: 和
和 . 下列说法正确的是:( )
. 下列说法正确的是:( )


- A、
- B、
- C、
- D、 无法判断
第八题
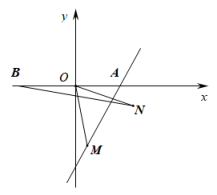
如图,在平面直角坐标系中,已知点P(0,2),点A(4,2).以点P为旋转中心,把点A按逆时针方向旋转60°,得点B.在M1(  ,0),M2(
,0),M2(  ,-1),M3(1,4),M4(2,
,-1),M3(1,4),M4(2,  )四个点中,直线PB经过的点是( )
)四个点中,直线PB经过的点是( )

- A、 M1
- B、 M2
- C、 M3
- D、 M4
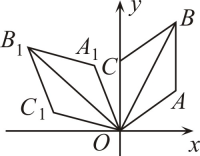
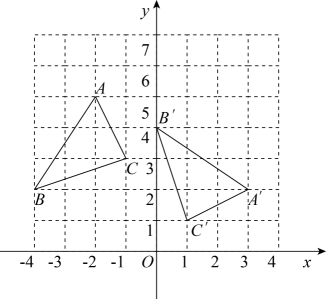
如图,在平面直角坐标系中, 的顶点都在方格纸的格点上,将
的顶点都在方格纸的格点上,将 绕着某点顺时针旋转一定的角度后,得到
绕着某点顺时针旋转一定的角度后,得到 , 则旋转中心的坐标为( )
, 则旋转中心的坐标为( )
- A、 (-1,1)
- B、 (-1,2)
- C、 (1,1)
- D、 (1,-1)
第九题
已知二次函数y=x2+ax+b(a,b为常数).命题①:该函数的图象经过点(1,0);命题②:该函数的图象经过点(3,0);命题③:该函数的图象与x轴的交点位于y轴的两侧;命题④;该函数的图象的对称轴为直线x=1.如果这四个命题中只有一个命题是假命题,则这个假命题是( )
- A、 命题①
- B、 命题②
- C、 命题③
- D、 命题④
关于二次函数y=(x﹣2)2+1,下列说法中错误的是( )
- A、 图象的开口向上
- B、 图象的对称轴为x=2
- C、 图象与y轴交于点(0,1)
- D、 图象可以由y=x2的图象向右平移2个单位长度,再向上平移1个单位长度得到
若二次函数  的图象与x轴有两个交点,满足条件的m的值是( )
的图象与x轴有两个交点,满足条件的m的值是( )
- A、 -2
- B、 0
- C、 1
- D、 2
已知抛物线 与
与 轴只有一个交点,且过点
轴只有一个交点,且过点 ,
,  , 则
, 则 的值为( )
的值为( )
- A、 -9
- B、 -16
- C、 -18
- D、 -27
若二次函数 满足
满足 . 下列四个结论,其中正确的是( )
. 下列四个结论,其中正确的是( )
- A、 若二次函数图象经过点
, 则
;
- B、 若
, 则方程
的根为
;
- C、 二次函数图象与
轴一定有两个交点;
- D、 点
,
在函数图象上,若
, 则当
时,
.
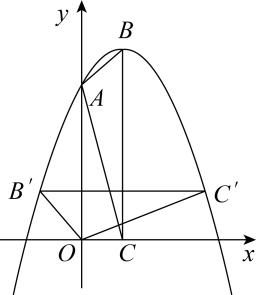
在平面直角坐标系中,已知点A(-2,3),B(2,1),若抛物线y=ax2-2x+1(a≠0)与线段AB有两个不同的交点,则a的取值范围是( )
- A、
- B、
- C、
- D、 a≤-1/2或a≥1
第十题
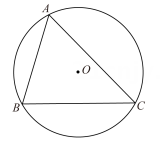
如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )
- A、 cosθ(1+cosθ)
- B、 cosθ(1+sinθ)
- C、 sinθ(1+sinθ)
- D、 sinθ(1+cosθ)
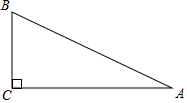
如图,在Rt△ABC中,直角边BC的长为m,∠A=40°,则斜边AB的长是( )
- A、 msin40°
- B、 mcos40°
- C、
- D、
如图,在⊙O中,弦 的长是
的长是 , 弦
, 弦 的弦心距为6cm,E是⊙O优弧
的弦心距为6cm,E是⊙O优弧 上一点.则
上一点.则 的度数为( )
的度数为( )

- A、 60°
- B、 45°
- C、 30°
- D、 80°
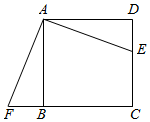
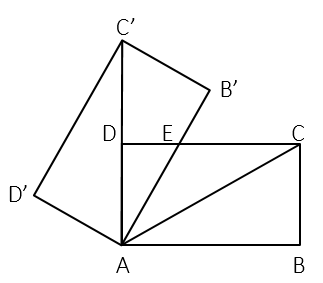
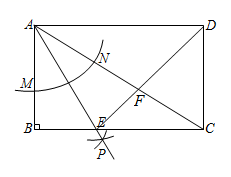
如图,在纸片  中,
中,  ,折叠纸片,使点
,折叠纸片,使点  落在
落在  的中点
的中点  处,折痕为
处,折痕为  ,则
,则  的面积为( )
的面积为( )

- A、
- B、
- C、
- D、