单选题
-5的相反数是( )
- A、 5
- B、 -5
- C、
- D、 -
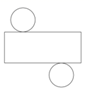
下列几何体的展开图中,能围成圆柱的是( )
- A、

- B、

- C、

- D、
将多项式 按x的降幂排列的结果为( )
按x的降幂排列的结果为( )
- A、
- B、
- C、
- D、
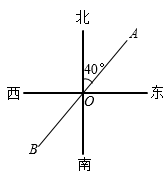
如图,直线AB经过点O,射线OA是北偏东40°方向,则射线OB的方位角是( )
- A、 南偏西50°
- B、 南偏西40°
- C、 北偏西50°
- D、 北偏西40°
下列计算正确的是( )
- A、 2x+4x=8x2
- B、 9x2y﹣9yx2=0
- C、 7x2﹣3x2=4
- D、 3x+2y=5xy
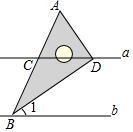
含30°角的直角三角板与直线a,b的位置关系如图所示,已知  ,
,  .则
.则  的度数是( )
的度数是( )
- A、 35°
- B、 45°
- C、 55°
- D、 65°
如图,点C、D为线段 上的两点,
上的两点, , 若
, 若 , 则
, 则 等于( )
等于( )
![]()
- A、 4
- B、 5
- C、 6
- D、 7
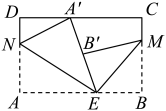
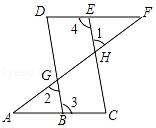
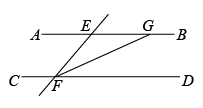
如图, ,
,  ,
,  平分
平分 , 则
, 则 的大小为( )
的大小为( )
- A、
- B、
- C、
- D、
按下面图示的程序计算,若开始输入的值x为正数,最后输出的结果为11,则满足条件的正数x有( )

- A、 1个
- B、 2个
- C、 3个
- D、 4个