单选题
嘉淇在证明“平行于同一条直线的两条直线平行”时,给出了如下推理过程:
已知:如图,b∥a,c∥a,求证:b∥c; 证明:作直线DF交直线a、b、c分 别于点D、E、F, ∵a∥b,∴∠1=∠4,又∵a∥c, ∴∠1=∠5, ∴b∥c.
|
小明为保证嘉淇的推理更严谨,想在方框中“∴∠1=∠5”和“∴b∥c”之间作补充,下列说法正确的是( )
- A、 嘉淇的推理严谨,不需要补充
- B、 应补充∠2=∠5
- C、 应补充∠3+∠5=180°
- D、 应补充∠4=∠5
阅读下列材料,其中①~④步数学依据错误的是( )
如图:已知直线 , a⊥b,求证:
.
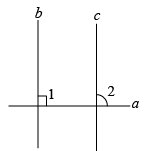
证明:∵(已知),
∴(①垂直的定义).
∵ (已知),
∴(②两直线平行,同位角相等),
∴(③同角的余角相等),
∴(④垂直的定义).
- A、 ①
- B、 ②
- C、 ③
- D、 ④
小英、小亮、小明和小华四名同学参加了“大梦杯”竞赛选拔赛,小亮和小华两个同学的得分和等于小明和小英的得分和;小英与小亮的得分和大于小明和小华的得分和;小华的得分超过小明与小亮的得分和.则这四位同学的得分由小到大的顺序是( )
- A、 小明、小亮、小华、小英
- B、 小明、小亮、小英、小华
- C、 小英、小华、小亮、小明
- D、 小亮、小英、小华、小明
有四位同学一起研究一道数学题.如图,已知EF⊥AB,CD⊥AB. 则下列说法正确的是( )
甲说:“如果还知道∠CDG=∠BFE, 则能得到∠AGD=∠ACB. ”
乙说:“把甲的已知和结论倒过来,即由∠AGD=∠ACB, 可得到∠CDG=∠BFE. ”
丙说:“∠AGD一定大于∠BFE. ”
丁说:“如果连接GF, 则GF一定平行于AB. ”

- A、 甲对乙错
- B、 乙错丁对
- C、 甲、乙对
- D、 乙、丙对
如图,四边形ABCD中,AC,BD交于点O, 如果∠BAC=∠DCA, 那么以下四个结论中错误的是( )

- A、AD∥BC
- B、AB∥CD
- C、 ∠ABD=∠CDB
- D、 ∠BAD+∠ADC=180°
下列推理中,错误的是( )
- A、 ∵AB=CD,CD=EF,∴AB=EF
- B、 ∵∠α=∠β,∠β=∠γ,∴∠α=∠γ
- C、 ∵a∥b,b∥c,∴a∥c
- D、 ∵AB⊥EF,EF⊥CD,∴AB⊥CD