单选题
设集合 ,
,  , 则
, 则 ( )
( )
- A、
- B、
- C、
- D、
设复数z满足 (i是虚数单位),则
(i是虚数单位),则 ( )
( )
- A、
- B、
- C、
- D、
在数列 中,“数列
中,“数列 是等比数列”是“
是等比数列”是“ ”的( )
”的( )
- A、 充分不必要条件
- B、 必要不充分条件
- C、 充要条件
- D、 既不充分也不必要条件
已知平面向量 ,
,  , 且
, 且 , 则
, 则 ( )
( )
- A、 1
- B、 14
- C、
- D、
某兴趣小组研究光照时长x(h)和向日葵种子发芽数量y(颗)之间的关系,采集5组数据,作如图所示的散点图.若去掉 后,下列说法正确的是( )
后,下列说法正确的是( )

- A、 相关系数r变小
- B、 决定系数
变小
- C、 残差平方和变大
- D、 解释变量x与预报变量y的相关性变强
已知 ,
,  , 且
, 且 , 则ab的最小值为( )
, 则ab的最小值为( )
- A、 4
- B、 8
- C、 16
- D、 32
如图,点 、
、 、
、 、
、 、
、 为正方体的顶点或所在棱的中点,则下列各图中,不满足直线
为正方体的顶点或所在棱的中点,则下列各图中,不满足直线 平面
平面 的是( )
的是( )
- A、

- B、

- C、
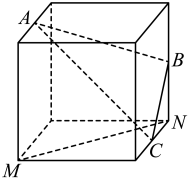
- D、

已知
 满足
满足 ,
,  且
且 在
在 上单调,则
上单调,则 的最大值为( )
的最大值为( )
- A、
- B、
- C、
- D、


