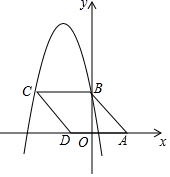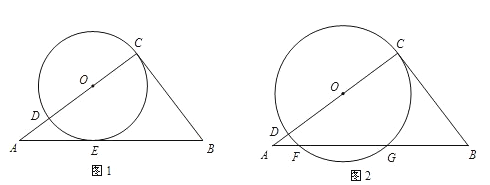2023年浙江省杭州市初中毕业生学业水平测试数学模拟试题(二)

下列实数： ， ， ， ， 中，无理数有（ ）个.

下列新冠疫情防控标识图案中，中心对称图形是（  ）

一个空间几何体的主视图和左视图都是边长为4的正三角形，俯视图是一个半径为2的圆，那么这个几何体的全面积是                      (   )

一组从小到大排列的数据：a，3，4，4，6(a为正整数)，唯一的众数是4，则该组数据的平均数是（   ）

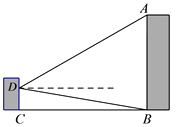
如图所示的几何体是由一些正方体组合而成的立体图形，则这个几何体的俯视图是（　　）

2022年上海疫情再起，经科学研究发现新病毒的直径是 ， 已知 ， 那么新冠病毒的直径用科学记数法表示为（    ）m．

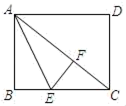
如图1，分别以直角三角形三边为边向外作等边三角形，面积分别为S₁、S₂、S₃；如图2，分别以直角三角形三个顶点为圆心，三边长为半径向外作圆心角相等的扇形，面积分别为S₄、S₅、S₆ ． 其中S₁=16，S₂=45，S₅=11，S₆=14，则S₃+S₄=（   ）

若实数、满足 ， 且、恰好是的两条边长，则第三条边长为（       ）．

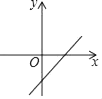
二次函数y=ax²+bx+c的图象如图所示，那么一次函数y=bx+a的图象大致是（    ）

如图，在平行四边形ABCD中，AB=6，∠BAD的平分线与BC的延长线交于点E，与DC交于点F，且AB=3CF，DG⊥AE，垂足为G，若DG=2，则AE的边长为（　　）

因式分解： ．

近似数13.7万精确到位.

一只盒子中有红球m个，白球8个，黑球n个，每个球除颜色不同外都相同，从中任取一个球，取得白球的概率与不是白球的概率相同，那么m与n的关系是．

如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C=20°，则∠CDA= .

如图，矩形纸片ABCD中，已知AD＝12，AB＝9，E是BC上的点，以AE为折痕折叠纸片，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为.

如图，在平面直角坐标系中，菱形ABCD的顶点A的坐标为（3，0），顶点B在y轴正半轴上，顶点D在x轴负半轴上．若抛物线y=-x²-5x+c经过点B、C，则菱形ABCD的面积为．

 

计算

2021年是中国共产党成立100周年，某校组织开展了丰富多彩的主题教育活动，活动设置了“A：诗歌朗诵表演，B：歌舞表演，C：书画作品展览，D：手工作品展览”四个专项活动，每个学生限选一个专项活动参与．为了解活动开展情况，学校随机抽取了部分学生进行调查，并根据调查结果绘制了如图所示的不完整的条形统计图和扇形统计图．

如图所示，某小组同学为了测量对面楼AB的高度，分工合作，有的组员测得两楼间距离为40米，有的组员在教室窗户处测得楼顶端A的仰角为30°，底端B的俯角为10°，请你根据以上数据，求出楼AB的高度．（精确到0.1米）

（参考数据：sin10°≈0.17， cos10°≈0.98， tan10°≈0.18， ≈1.41， ≈1.73）

已知直线y=kx+b经过点A（﹣3，﹣8），且与直线 的公共点B的横坐标为6．

已知，Rt△ABC中，∠C=90°，AC=4，BC=3．以AC上一点O为圆心的⊙O与BC相切于点C，与AC相交于点D．

（1）如图1，若⊙O与AB相切于点E，求⊙O的半径；

（2）如图2，若⊙O在AB边上截得的弦FG= ， 求⊙O的半径．

如图，在△ABC中，点D、E分别是边BC、AC的中点，过点A作AF∥BC，与DE的延长线相交于点F，连接CF．

（1）求证：四边形ABDF是平行四边形；

（2）若∠CAF=45°，BC=AC，直接写出图中（不添加其它线段）等于67.5°的所有角．

如图①所示，已知A、B为直线L上两点，点C为直线L上方一动点，连接AC、BC，分别以AC、BC为边向ABC外作正方形CADF和正方形CBEG，过点D作DD_1l于点D₁ ， 过点E作EE₁l于点E₁.
（1）如图②，当点E恰好在直线l上时(此时E₁与E重合)，试说明DD₁=AB；
（2）在图①中，当D、E两点都在直线l的上方时，试探求三条线段DD₁、EE₁、AB之间的数量关系，并说明理由；
（3）如图③，当点E在直线l的下方时，请直接写出三条线段DD₁、EE₁、AB之间的数量关系.(不需要证明)