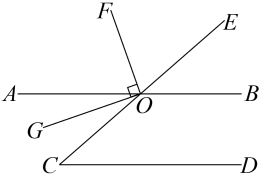
两直线平行,同位角相等
两直线平行,内错角相等
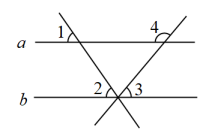
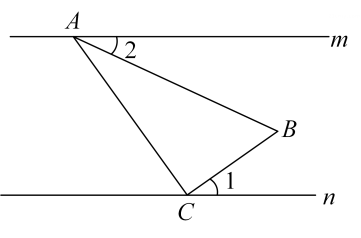
如图,一块含有45°角的直角三角板的两个顶点放在直尺的对边上.若∠1=21°,则∠2度数为( )
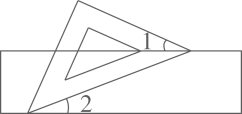
- A、 21°
- B、 22°
- C、 23°
- D、 24°
两直线平行,同旁内角互补
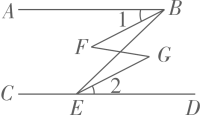
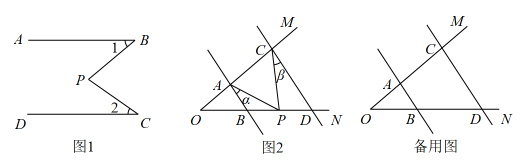
如图, ,
,  .若
.若 , 则
, 则 的大小为( )
的大小为( )

- A、
- B、
- C、
- D、
平行线的拐点辅助线
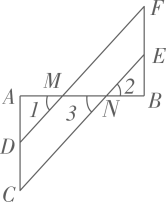
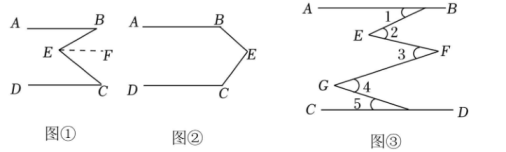
如图,AB∥DE,BC⊥CD,则以下说法中正确的是( )

- A、 α,β的角度数之和为定值
- B、 α随β增大而增大
- C、 α,β的角度数之积为定值
- D、 α随β增大而减小
综合训练
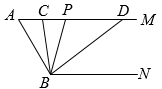
如图,在四边形 中,
中, ,
,  平分
平分 ,
,  ,
,  , 点H在直线
, 点H在直线 上,满足
上,满足 . 若
. 若 , 则k的值是( )
, 则k的值是( )

- A、
和
- B、
和
- C、
和
- D、
和
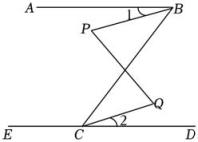
如图, ,
,  , 探索图中角α,β,γ之间的关系式正确的是( )
, 探索图中角α,β,γ之间的关系式正确的是( )

- A、
- B、
- C、
- D、