选择题
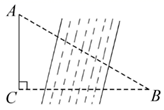
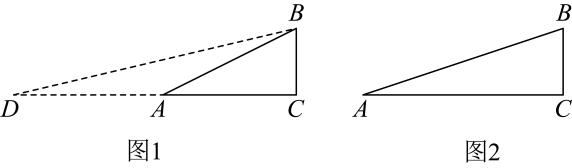
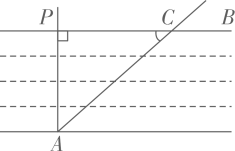
以下是某数学兴趣小组开展的课外探究活动,探究目的:测量小河两岸的距离,探究过程:在河两岸选取相对的两点P、A,在小河边取 的垂线
的垂线 上的一点C,测得
上的一点C,测得 米,
米, , 则小河宽
, 则小河宽 等于( )
等于( )
- A、
米
- B、
米
- C、
米
- D、
米
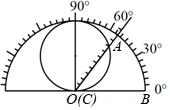
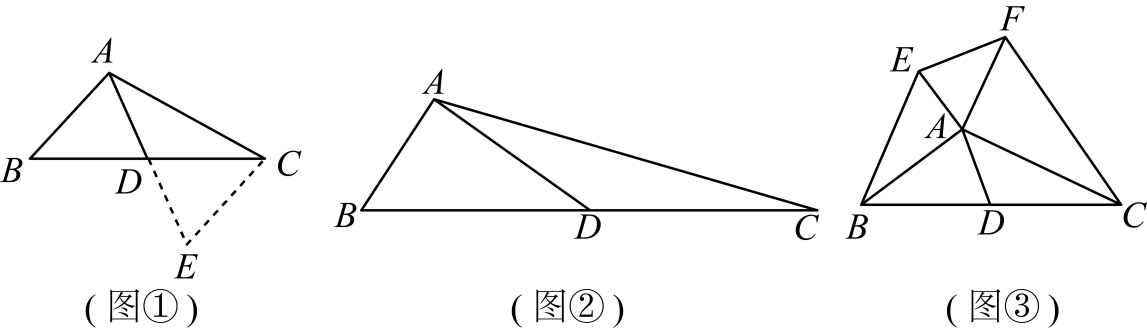
探究;我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等.例如在△ABC中,∠A=30°,AC=3,∠A所对的边为 , 满足已知条件的三角形有两个(我们发现其中一个△ABC是直角三角形,如图),则满足已知条件的三角形的第三边AB的长为( )
, 满足已知条件的三角形有两个(我们发现其中一个△ABC是直角三角形,如图),则满足已知条件的三角形的第三边AB的长为( )

- A、
- B、
- C、
或
- D、
或
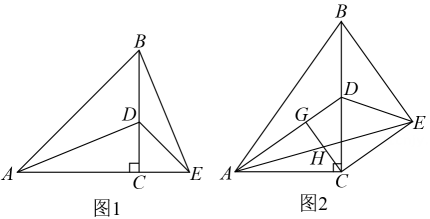
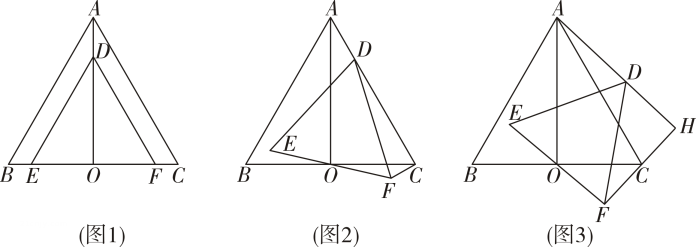
在数学活动课上,老师出示两张等腰三角形纸片,如图所示.图1的三角形边长分别为4,4,2;图2的三角形的腰长也为4,底角等于图1中三角形的顶角;某学习小组将这两张纸片在同一平面内拼成如图3的四边形OABC,连结AC.该学习小组经探究得到以下四个结论,其中错误的是( )
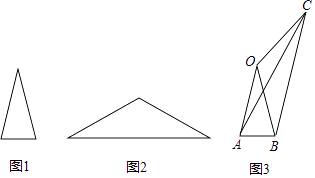
- A、 ∠OCB=2∠ACB
- B、 ∠OAB+∠OAC=90°
- C、 AC=2
- D、 BC=4