选择题
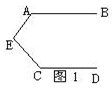
如图, ,
,  与
与 的角平分线交于点G,且
的角平分线交于点G,且 , 已知
, 已知 , 若
, 若 ,
,  , 则下列等式中成立的是( )
, 则下列等式中成立的是( )

- A、
- B、
- C、
- D、
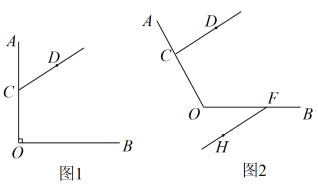
如图,已知 , 若按图中规律继续划分下去,则
, 若按图中规律继续划分下去,则 等于( )
等于( )

- A、
- B、
- C、
- D、
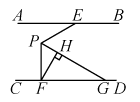
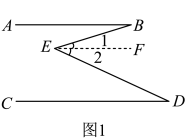
已知 , 点E在
, 点E在 连线的右侧,
连线的右侧, 与
与 的角平分线相交于点F,则下列说法正确的是( );
的角平分线相交于点F,则下列说法正确的是( );
①;
②若 , 则
;
③如图(2)中,若 ,
, 则
;
④如图(2)中,若 ,
, 则
.

- A、 ①②④
- B、 ②③④
- C、 ①②③
- D、 ①②③④