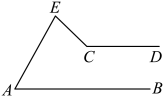
猪蹄模型
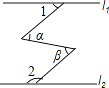
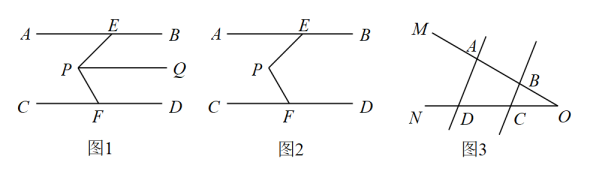
如图,已知AB∥EF.若∠C=90°,则∠α,∠β,∠γ之间的关系是( )

- A、 ∠β=∠α+∠γ
- B、 ∠α+∠β+∠γ=180°
- C、 ∠α+∠β-∠γ=90°
- D、 ∠β+∠γ-∠α=90°
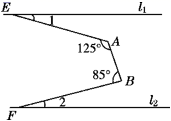
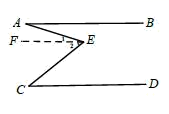
如图,AB∥EF, 则∠A、∠C、∠D、∠E满足的数量关系是( )
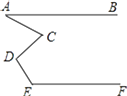
- A、 ∠A+∠C+∠D+∠E=360°
- B、 ∠A+∠D=∠C+∠E
- C、 ∠A-∠C+∠D+∠E=180°
- D、 ∠E-∠C+∠D-∠A=90°
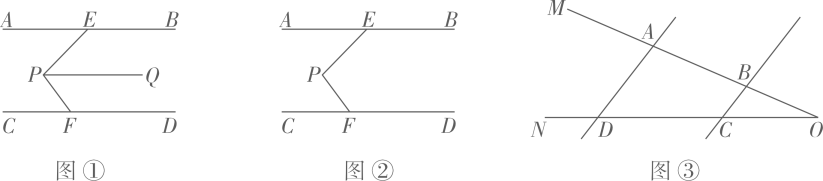
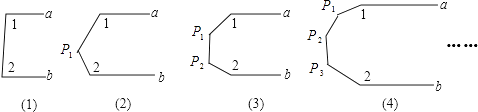
如图,若 , 用含有∠1,∠2,∠3的式子表示∠α,则∠α应为( )
, 用含有∠1,∠2,∠3的式子表示∠α,则∠α应为( )

- A、
- B、
- C、
- D、
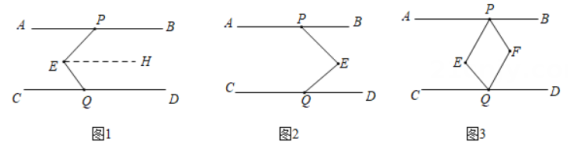
①如图1, , 则
, 则 ;②如图2,
;②如图2, , 则
, 则 ;③如图3,
;③如图3, , 则
, 则 ;④如图4,
;④如图4, , 则
, 则 . 以上结论正确的个数是( )
. 以上结论正确的个数是( )

- A、 ①②③④
- B、 ①②③
- C、 ②③④
- D、 ①②④
铅笔头模型
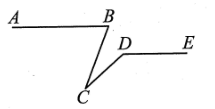
如图:已知  ,
,  度,
度,  度,则
度,则  等于( )度.
等于( )度.
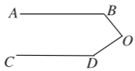
- A、 50
- B、 60
- C、 80
- D、 90
如图,已知A1B∥AnC,则∠A1+∠A2+…+∠An等于( )
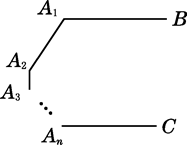
- A、 180°n
- B、 (n+1)·180°
- C、 (n-1)·180°
- D、 (n-2)·180°
如图,已知 , 若按图中规律继续划分下去,则
, 若按图中规律继续划分下去,则 等于( )
等于( )

- A、
- B、
- C、
- D、