选择题
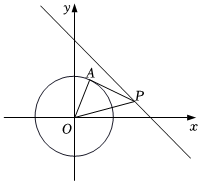
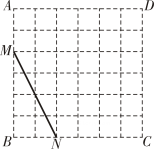
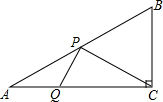
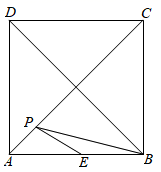
如图,▱ABCD中,AB=3,AD=5,AC⊥AB , E、F为线段BD上两动点(不与端点重合)且EF= BD , 连接AE , CF , 当点EF运动时,对AE+CF的描述正确的是( )
BD , 连接AE , CF , 当点EF运动时,对AE+CF的描述正确的是( )
- A、 等于定值5-
- B、 有最大值
- C、 有最小值
- D、 有最小值
如图,在边长为a的正方形 中,E是对角线
中,E是对角线 上一点,且
上一点,且 , 点P是
, 点P是 上一动点,则点P到边
上一动点,则点P到边 ,
,  的距离之和
的距离之和 的值( )
的值( )

- A、 有最大值a
- B、 有最小值
- C、 是定值a
- D、 是定值
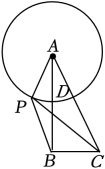
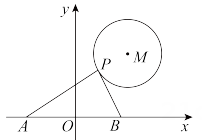
如图,AB为⊙O的直径,AB=8,点C为半圆AB上一动点,以BC为边向⊙O外作正ΔBCD(点D在直线AB的上方),连接OD,则线段OD的( )
- A、 随点C的运动而变化,最小值为

- B、 随点C的运动而变化,最大值为8
- C、 随点C的运动而变化,最大值为

- D、 随点C的运动而变化,但无最值
如图,在矩形ABCD中,AB=4,AD=6,点P在AD上,点Q在BC上,且AP = CQ,连接CP,QD,则PC + QD的最小值为( )

- A、 8
- B、 10
- C、 12
- D、 20
在周长为  的正方形
的正方形  中,点
中,点  是
是  边的中点,点
边的中点,点  为对角线
为对角线  上的一个动点,则
上的一个动点,则  的最小值为( )
的最小值为( )
- A、 2
- B、
- C、
- D、
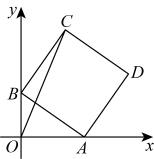
如图,矩形 中,
中, ,
,  , G是
, G是 的中点,线段
的中点,线段 在边
在边 上左右滑动,若
上左右滑动,若 , 则
, 则 的最小值为( )
的最小值为( )

- A、 4
- B、 5
- C、
- D、
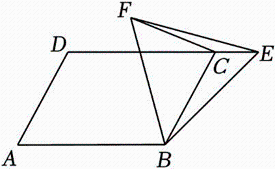
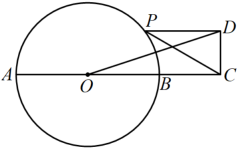
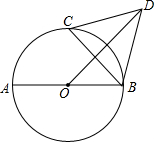
如图,AB是⊙O的直径,AB=10,点C是圆上不与A , B重合的点,CD平分∠ACB , 交⊙O于D , AE平分∠CAB , 交CD于E . 有以下说法:
①点D是定点;
②AC•BC的最大值为50;
③D为△ABE的外心;
④CA+CB的最大值为 .
其中正确的有( )

- A、 1个
- B、 2个
- C、 3个
- D、 4个
如图, 的半径
的半径 弦
弦 于点E , C是
于点E , C是 上一点,
上一点, ,
,  的最大值为18,则
的最大值为18,则 的长为( )
的长为( )


- A、 8
- B、 6
- C、 4
- D、 2
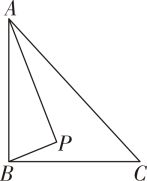
如图, 中,
中, ,
,  , 则边
, 则边 的最大值为( )
的最大值为( )

- A、
- B、
- C、 8
- D、
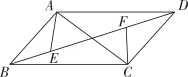
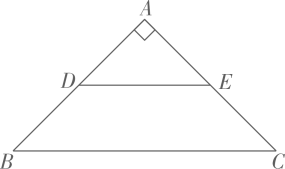
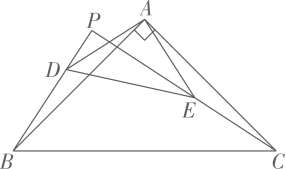
如图,在 中,
中, , 点D、E分别是
, 点D、E分别是 的中点.将
的中点.将 绕点A顺时针旋转
绕点A顺时针旋转 , 射线
, 射线 与射线
与射线 交于点P,在这个旋转过程中有下列结论:
交于点P,在这个旋转过程中有下列结论:
①;②
存在最大值为
;③
存在最小值为
;④点P运动的路径长为
. 其中,正确的是( )
- A、 ①③④
- B、 ①②④
- C、 ①②③
- D、 ②③④