选择题（每题3分，共30分）
两个直角三角形全等的条件是（ ）
- A、 一个锐角对应相等
- B、 一条边对应相等
- C、 两条直角边对应相等
- D、 两个角对应相等
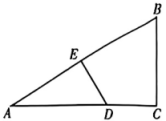
如图，最适合用“HL”定理判定Rt△ABC和Rt△DEF全等的条件是（ ）
- A、 AC=DF，BC=EF．
- B、 ∠A=∠D，AB=DE．
- C、 AC=DF，AB=DE．
- D、 ∠B=∠E，BC= EF．
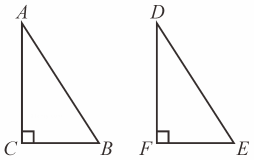
如图，已知点A、D、C、F在同一条直线上，∠B＝∠E＝90°，AB=DE，若添加一个条件后，能用“HL”的方法判定Rt△ABC≌Rt△DEF ， 添加的条件可以是（ ）
- A、 BC＝EF
- B、 ∠BCA＝∠F
- C、 AB∥DE
- D、 AD＝CF
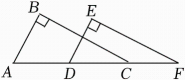
如图，
于点D，
于点F，
． 要根据“
”证明
， 则还需要添加的条件是（ ）
- A、
- B、
- C、
- D、
在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，下列条件中不能判定Rt△ABC≌Rt△A′B′C′的是（ ）
- A、 AC=A′C′，∠B=∠B′
- B、 ∠A=∠A′，∠B=∠B′
- C、 AB=A′B′，AC=A′C′
- D、 AB=A′B′，∠A=∠A′
如图，在△ABC中，AB=AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别是E，F．下列结论中，不正确的是（ ）
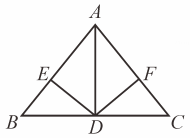
- A、 DA平分∠EDF
- B、 AE=AF
- C、 AD上任一点P到AB，AC的距离相等
- D、 AB，AC上的点到AD的距离相等
在 
中，已知 
，AD是 的角平分线， 
于点E.若 的面积为S，则 
的面积为（ ）
- A、
- B、
- C、
- D、
如图，△ABD和△CBD，∠ADB=90°，∠ABD=∠DBC，AD=DC=1，若AB=4，则BC的长为（ ）
- A、
- B、 2
- C、 3
- D、
