如图所示，在正方形ABCD中，AB=1，点P是对角线AC上的一点，分别以AP，PC为对角线作正方形，则两个小正方形的周长的和是（ ）
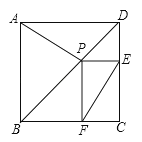
如图，在正方形ABCD中，AB=4，P是线段AD上的动点，PE⊥AC于点E，PF⊥BD于点F，则PE+PF的值为（ ）
已知在正方形ABCD中，对角线AC与BD相交于点O，OE∥AB交BC于点E，若AD=8cm，则OE的长为（ ）
如图，正方形ABCD中，AE=AB，直线DE交BC于点F，则∠BEF=（ ）
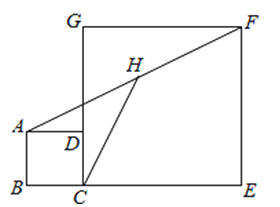
如图，边长分别为4和8的两个正方形ABCD和CEFG并排放在一起，连接BD并延长交BG于点T，交FG于点P，则ET的值为（ ）
如图，下列四组条件中，能判定▱ABCD是正方形的有（ ）
①AB=BC，∠A=90°；②AC⊥BD，AC=BD；③OA=OD，BC=CD；④∠BOC=90°，∠ABD=∠DCA．
如图，在四边形ABCD中，AB＝BC＝CD＝DA ， 对角线AC与BD相交于点O ， 若不增加任何字母与辅助线，要使四边形ABCD是正方形，则还需增加一个条件是
如图，在Rt△ABC中，∠C＝90°，DE垂直平分AC ， DF⊥BC ， 当△ABC满足条件时，四边形DECF是正方形．（要求：①不再添加任何辅助线，②只需填一个符合要求的条件）
如图，边长分别为3和5的两个正方形ABCD和CEFG并排放在一起，连结BD并延长交EG于点T，交FG于点P，则ET的长为
如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是 ．
如图，正方形ABCD中，AB=1，点P是对角线AC上的一点，分别以AP、PC为对角线作正方形，则两个小正方形的周长的和是 ．
如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，连接BE、DF，DF交对角线AC于点G，且DE=DG．
（1）求证：AE=CG；
（2）试判断BE和DF的位置关系，并说明理由．
如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，联结BE、DF，DF交对角线AC于点G，且DE=DG；
（2）求证：BE∥DF．
如图，点B、C、E是同一直线上的三点，四边形ABCD与四边形CEFG都是正方形，连接BG、DE．
（1）求证：BG=DE；
（2）已知小正方形CEFG的边长为1cm，连接CF，如果将正方形CEFG绕点C逆时针旋转，当A、E两点之间的距离最小时，求线段CF所扫过的面积．
已知：P是正方形ABCD对角线BD上一点，PE⊥DC，PF⊥BC，E、F分别为垂足．
求证：AP=EF．
已知，在正方形ABCD中，E是CB延长线上一点，且EB=BC，F是AB的中点，请你将F点与图中某一标明字母的点连接成线段，使连成的线段与AE相等．并证明这种相等关系．
