选择题。
抛物线y=(x-2)2的对称轴是( )
- A、 直线x=-1
- B、 直线x=1
- C、 直线x=-2
- D、 直线x=2
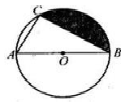
如图。已知点A,B,C在圆O上.若∠ACB=50°,则∠AOB的度数是( )

- A、 100°
- B、 1050°
- C、 110°
- D、 130°
将抛物线y=x2向上平移两个单位,得到的新抛物线的函数表达式为( )
- A、 y=x2-2
- B、 y=x2+2
- C、 y=(z-2)2
- D、 y=(x+2)2
已知圆O的半径为10,弦AB=16,则圆心O到弦AB的距离是( )
- A、
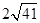
- B、

- C、 12
- D、 6
有一种纸上游戏叫“划蟹脚”,如图,每个数字连线着一个任务(任务不可见),参与者选一个数字(即“蟹脚”)划去,已划去的数字不能再划,所有人划完后任务公开,每个人执行所划数字对应的任务.小丽随机划去一个数字,则她执行“扫地”任务的概率是( )
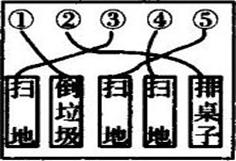
- A、
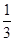
- B、
- C、
- D、 1
如图,矩形ABCD中,AB=9,BC=6,点E.F分别是边BC,CD上的点.且AE⊥EF,则AF的最小值是( )

- A、 10
- B、
- C、

- D、 9
如图·在Rt△ABC中,∠C=90°,AC=6,BC=8.在△ABC内放入边长为1的正方形纸片,每两张纸片都不重叠,则最多能放入的正方形纸片的张数是( )
![]()
- A、 15
- B、 16
- C、 17
- D、 18