单选题
设集合  ,则
,则  ( )
( )
- A、
- B、
- C、
- D、
已知复数  满足
满足  ,则
,则  ( )
( )
- A、
- B、
- C、
- D、
已知命题  ,那么
,那么  是( )
是( )
- A、
- B、
- C、
- D、
图1是某学习小组学生数学考试成绩的茎叶图,1号到16号的同学的成绩依次为  ,图2是统计茎叶图中成绩在一定范围内的学生情况的程序框图,那么该程序框图输出的结果是( )
,图2是统计茎叶图中成绩在一定范围内的学生情况的程序框图,那么该程序框图输出的结果是( )

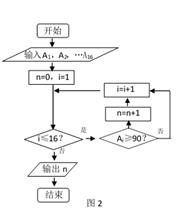
- A、 6
- B、 7
- C、 10
- D、 16
已知  ,且
,且  ,则
,则  ( )
( )
- A、
- B、
- C、
- D、
设  ,则
,则  的大小关系为( )
的大小关系为( )
- A、
- B、
- C、
- D、
设函数  的最小正周期为
的最小正周期为  ,且
,且  ,则 ( )
,则 ( )
- A、
在
上单调递减
- B、
在
上单调递减
- C、
在
上单调递增
- D、
在
上单调递增
已知三棱锥的三视图如图所示,则该三棱锥外接球的表面积为( )

- A、
- B、
- C、
- D、
已知点  ,过抛物线
,过抛物线  上一点
上一点  的直线与直线
的直线与直线  垂直相交于点
垂直相交于点  ,若
,若  ,则
,则  的横坐标为( )
的横坐标为( )
- A、
- B、 2
- C、
- D、 1
已知关于  的方程
的方程  有2个不相等的实数根,则
有2个不相等的实数根,则  的取值范围是( ).
的取值范围是( ).
- A、
- B、
- C、
- D、



