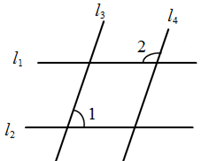单选题
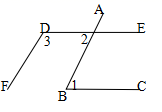
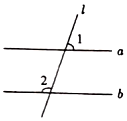
如图,已知a∥b,l与a,b相交.若∠1=70°,则∠2等于( )
- A、 .120°
- B、 110°
- C、 .100°
- D、 .70°
如图,若直线  ,则下列各式成立的是( )
,则下列各式成立的是( )
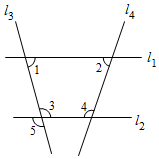
- A、
- B、
- C、
- D、
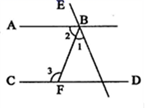
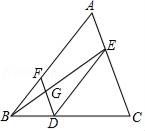
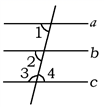
如图,下列推理错误的是( )
- A、 ∵
,
- B、 ∵
- C、
- D、 ∵
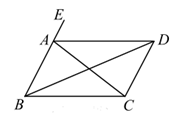
如图,已知  ,则下列结论中正确的是( )
,则下列结论中正确的是( )
- A、
- B、
- C、
- D、
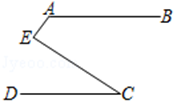
如图,AB∥CD,∠BAE=120°,∠DCE=30°,则∠AEC=( )度.
- A、 70
- B、 150
- C、 90
- D、 100
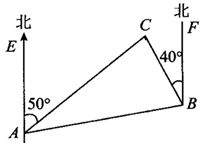
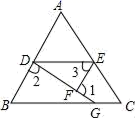
若一副三角板按如图所示放置,则∠EGA的度数为( )

- A、 30°
- B、 45°
- C、 60°
- D、 75°
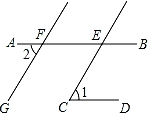
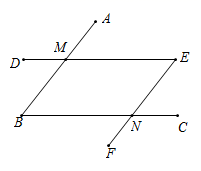
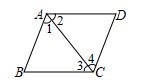
如图,由AB∥CD,可以得到( )
- A、 ∠1=∠2
- B、 ∠2=∠3
- C、 ∠1=∠4
- D、 ∠3=∠4
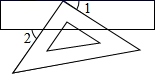
如图,三角板的直角顶点落在矩形纸片的一边上.若  ,则
,则  的度数是( )
的度数是( )
- A、
- B、
- C、
- D、
如图,AB∥CD,∠EFD=64°,∠FEB的角平分线EG交CD于点G,则∠GEB的度数为( )

- A、 66°
- B、 56°
- C、 68°
- D、 58°