单选题
下列运用等式性质进行的变形中,正确的是( )
- A、 若a=b,则ac=bc
- B、 若x=y,则5﹣x=5+y
- C、 若2x=3,则x=
- D、 若a=b,则
=
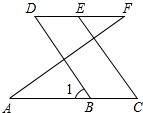
如图,下列判断正确的是( )
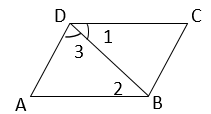
- A、 若∠1=∠2,则AD∥BC
- B、 若∠1=∠2,则AB∥CD
- C、 若∠A=∠3,则AD∥BC
- D、 若∠3+∠ADC=180° ,则AB∥CD
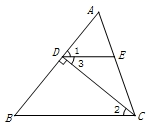
如图,在  中,
中,  是
是  延长线上点,
延长线上点,  ,
,  ,则
,则  等于( )
等于( )
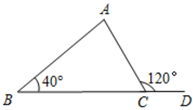
- A、 50°
- B、 60°
- C、 70°
- D、 80°
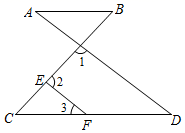
如图,点  在
在  的延长线上,下列条件不能判断
的延长线上,下列条件不能判断  的是( )
的是( )

- A、
- B、
- C、 ∠5=∠B
- D、
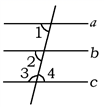
如图,直线a,b被直线c所截,下列条件能判断a∥b的是( )
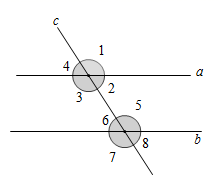
- A、 ∠3=∠5
- B、 ∠4=∠7
- C、 ∠2+∠3=180°
- D、 ∠1=∠3
如图,已知直线  ,
,  ,
,  ,则
,则  等于( )
等于( )
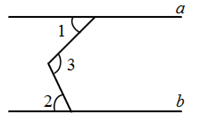
- A、 110°
- B、 100°
- C、 130°
- D、 120°
如图,AB和CD相交于点O,则下列结论正确的是( )

- A、 ∠1=∠2
- B、 ∠2=∠3
- C、 ∠3=∠4
- D、 ∠1=∠5
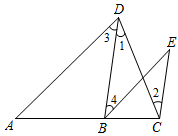
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BAD=180°,其中能推出  的是( )
的是( )

- A、 ①②
- B、 ①③
- C、 ②③
- D、 ②④
如图,下列推理错误的是( )
- A、 ∵
,
- B、 ∵
- C、
- D、 ∵
如图,已知  .则结论①
.则结论①  ;②
;②  平分
平分  ;③
;③  ;④
;④ 
 .正确的是( )
.正确的是( )

- A、 ①②③
- B、 ①②④
- C、 ①③④
- D、 ②③④