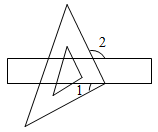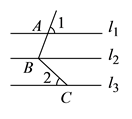单选题
如图,若直线  ,则下列各式成立的是( )
,则下列各式成立的是( )
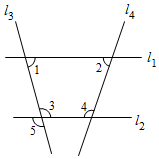
- A、
- B、
- C、
- D、
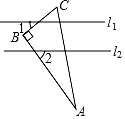
如图,已知直线l1∥l2 , 将一块直角三角板ABC按如图所示方式放置,若∠1=39°,则∠2等于( )
- A、 39°
- B、 45°
- C、 50°
- D、 51°
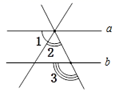
如图,a∥b,M、N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3=( ).
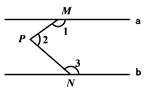
- A、 180°
- B、 360°
- C、 270°
- D、 540°
如图,如果AB∥EF,EF∥CD,下列各式正确的是( )

- A、 ∠1+∠2−∠3=90°
- B、 ∠1−∠2+∠3=90°
- C、 ∠1+∠2+∠3=90°
- D、 ∠2+∠3−∠1=180°
如图,已知a∥b,∠1=50°,∠3=10°,则∠2等于( )

- A、 30°
- B、 40°
- C、 50°
- D、 60°
如图,已知a//b,且∠2比∠1的2倍少6°,那么∠2的度数为( )

- A、 106°
- B、 112°
- C、 118°
- D、 124°
如图,已知:AD∥BC,AB∥CD,BE平分∠ABC,EC平分∠BED,∠ECD=45°,则∠ABC的度数为( )

- A、 45°
- B、 52°
- C、 56°
- D、 60°