黑龙江省佳木斯市前进区2021-2022学年九年级上学期期末数学试题

到2020年底我国脱贫攻坚战取得全面胜利，现行标准下98990000农村贫困人口全部脱贫，将数据98990000科学记数法表示为．

函数中，自变量x取值范围是．

如图，点 ， 分别在△ 的 ， 边上．只需添加一个条件即可证明△ ∽△ ，这个条件可以是．（写出一个即可）

小明和小亮在玩“石头、剪子、布”的游戏，两人一起做同样手势的概率是．

若不等式组无解，则m的取值范围是．

如图，点A、B、C是半径为4的⊙O上的三个点，若∠BAC＝45°，则弦BC的长等于．

一个圆锥的底面圆半径为6cm，圆锥侧面展开图扇形的圆心角为240°，则圆锥的母线长为 cm．

如图，AB是半圆O的直径，AB＝4，点C，D在半圆上，OC⊥AB， ， 点P是OC上的一个动点，则BP＋DP的最小值为．

如图，矩形ABCD中，AD＝4，AB＝10，P为CD边上的动点，当DP＝时，△ADP与△BCP相似．

如图，在x轴的正半轴上依次截取OA₁＝A₁A₂＝A₂A₃ ， …，过点A₁、A₂、A₃、…分别作x轴的垂线与反比例函数y（x≠0）的图象相交于点P₁、P₂、P₃、…，得直角三角形OP₁A₁、A₁P₂A₂、A₂P₃A₃、…，设其面积分别为S₁、S₂、S₃、…，则Sn的值为．

下列运算正确的是（    ）

下列标志是中心对称图形，但不是轴对称图形的是（    ）

八个大小相同的正方体搭成的几何体如图所示，其主视图是（    ）

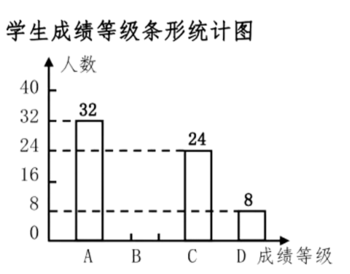
在春季运动会中，有9名学生参加100米比赛，并且他们的最终成绩各不相同，若一名学生想知道自己能否进入前5名，除了要了解自己的成绩外，还要了解这9名学生成绩的（    ）

新型冠状病毒肺炎具有人传人性，调查发现1人感染病毒后如果不隔离，那么经过两轮传染将会有225人感染，若设1人平均感染x人，则x为（   ）

已知关于 的分式方程 的解是非正数，则m的取值范围是（  ）

周末，小明的妈妈让他到药店购买口罩和消精湿巾，已知口罩每包3元，酒精湿巾每包2元，共用了30元钱（两种物品都买），小明的购买方案共有（    ）

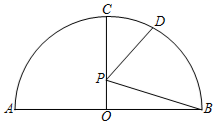
如图，点P在反比例函数y= （k≠0）的图象上，PA⊥x轴于点A，△PAO的面积为2，则k的值为（　　）

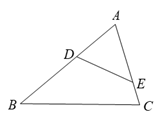
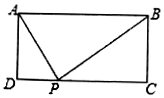
如图，点P是▱ABCD边AD上的一点，E，F分别是BP，CP的中点，已知▱ABCD面积为16，那么△PEF的面积为（    ）

在锐角△ABC中，∠BAC＝60°，BN、CM为高，P为BC的中点，连接MN、MP、NP，则结论：①NP＝MP；②AN：AB＝AM：AC；③BN＝2AN；④当∠ABC＝60°时，MN∥BC，一定正确的有（    ）

先化简，再求值： ，其中x=tan60°．

如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，△ABC的三个顶点坐标分别为A（1，4），B（1，1），C（3，1）．

⑴画出△ABC关于x轴对称的△A₁B₁C₁；

⑵画出△ABC绕点O逆时针旋转90°后的△A₂B₂C₂；

⑶在（2）的条件下，求线段BC扫过的面积（结果保留π）．

如图，抛物线y＝＋bx＋c经过坐标原点，并与x轴交于点A（2，0）．

学史明理，学史增信，学史崇德，学史力行，在建党100周年之际，某校对全校学生进行了一次党史知识测试，成绩评定共分为A，B，C，D四个等级，随机抽取了部分学生的成绩进行调查，将获得的数据整理绘制成如下两幅不完整的统计图．

根据统计图提供的信息，解答下列问题：

小明一家利用元旦三天驾车到某景点旅游．小汽车出发前油箱有油36L， 行驶，若干小时后，途中在加油站加油若干升，油箱中余油量Q（L）与行驶时间t（h）之间的关系，如图所示，根据图象回答下列问题；

已知∠ACD＝90°，MN是过点A的直线，AC＝DC，且DB⊥MN于点B，如图易证BD＋ABCB，过程如下：

解：过点C作CE⊥CB于点C，与MN交于点E

∵∠ACB＋∠BCD＝90°，∠ACB＋∠ACE＝90°，

∴∠BCD＝∠ACE．

∵DB⊥MN，∴∠ABC＋∠CBD＝90°，

CE⊥CB，∴∠ABC＋∠CEA＝90°，

∴∠CBD＝∠CEA．

又∵AC＝DC，

∴△ACE≌△DCB（AAS），

∴AE＝DB，CE＝CB，

∴△ECB为等腰直角三角形，

∴BECB．

又∵BE＝AE＋AB，∴BE＝BD＋AB，

∴BD＋ABCB．

某企业准备购买一批爱心物资捐赠给学校.经了解，若购买洗手液300瓶和口罩200包，则共需6000元；若购买洗手液500瓶和口罩300包，则共需9500元.

已知：如图，在平面直角坐标系中，点A，B分别在x，y轴上，且OA，OB的长（OA＞OB）是一元二次方程x²﹣7x＋12＝0的两根．