苏科版初中数学七年级下册 12.2 证明同步训练（基础版）

作者UID:11525262

日期: 2024-11-04

同步测试

单选题

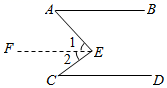
用反证法证明命题：“如图，如果AB//CD，AB//EF，那么CD//EF.”证明的第一个步骤是（）

A、假定CD//EF

B、假定CD不平行于EF

C、已知AB//EF

D、假定AB不平行于EF

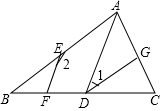
定理：三角形的一个外角等于与它不相邻的两个内角的和．已知：如图，∠ACD是△ABC的外角．求证：∠ACD＝∠A+∠B．

证法1：如图，

∵∠A＝70°，∠B＝63°，

且∠ACD＝133°（量角器测量所得）

又∵133°＝70°+63°（计算所得）

∴∠ACD＝∠A+∠B（等量代换）．

证法2：如图，

∵∠A+∠B+∠ACB＝180°（三角形内角和定理），

又∵∠ACD+∠ACB＝180°（平角定义），

∴∠ACD+∠ACB＝∠A+∠B+∠ACB（等量代换）．

∴∠ACD＝∠A+∠B（等式性质）．

下列说法正确的是（）

A、证法1用特殊到一般法证明了该定理

B、证法1只要测量够100个三角形进行验证，就能证明该定理

C、证法2还需证明其他形状的三角形，该定理的证明才完整

D、证法2用严谨的推理证明了该定理

在探究证明“三角形的内角和是180°”时，综合实践小组的同学作了如下四种辅助线，其中不能证明“三角形内角和是180°”的是（）

如图，给出下列条件：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ，且 $\text{[math]}$ ；④ $\text{[math]}$ 且 $\text{[math]}$ ；其中能推出 $\text{[math]}$ 的条件为（）

阅读下列材料，其①～④步中数学依据错误的是（）

如图：已知直线 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ .

证明：①∵ $\text{[math]}$ （已知）

∴ $\text{[math]}$ （垂直的定义）

②又∵ $\text{[math]}$ （已知）

③∴ $\text{[math]}$ （同位角相等，两直线平行）

∴ $\text{[math]}$ （等量代换）

④∴ $\text{[math]}$ （垂直的定义）.

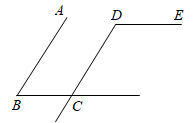
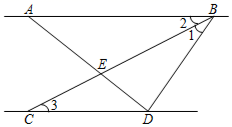
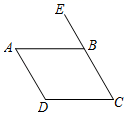
如图，点E在BA的延长线上，能证明BE∥CD是（）

A、 ∠EAD=∠B

B、 ∠BAD=∠BCD

C、 ∠EAD=∠ADC

D、 ∠BCD+∠D=180°

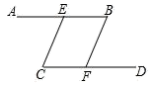
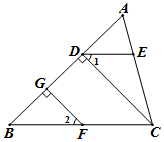
如图，下列条件中能证明AD $\text{[math]}$ BC的是（）

A、 ∠A＝∠C

B、 ∠ABE＝∠C

C、 ∠A+∠D＝180°

D、 ∠C+∠D＝180°

已知a，b，c是三条直线，下列结论正确的是（）

A、若a∥b，b∥c，则a∥c

B、若a⊥b，b⊥c，则a⊥c

C、若a∥b，b⊥c，则a∥c

D、若a⊥b，b∥c，则a∥c

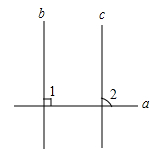
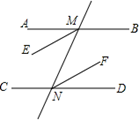
如图，下列推理及所证明的理由都正确的是（）

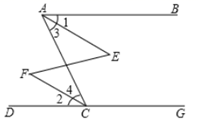
A、若 $\text{[math]}$ ，则 $\text{[math]}$ ，理由是内错角相等，两直线平行

B、若 $\text{[math]}$ ，则 $\text{[math]}$ ，理由是两直线平行，内错角相等

C、若 $\text{[math]}$ ，则 $\text{[math]}$ ，理由是内错角相等，两直线平行

D、若 $\text{[math]}$ ，则 $\text{[math]}$ ，理由是两直线平行，内错角相等

下列选项中，可以用来证明命题“若a2-4a=0，则a=0”是假命题的反例是（）.

填空题

命题“若x（1﹣x）＝0，则x＝0”是命题（填“真”、假），证明时可举出的反例是．

完成下面的证明：已知：如图， $\text{[math]}$ ．求证： $\text{[math]}$ ∥ $\text{[math]}$ ．

证明：过点 $\text{[math]}$ 作 $\text{[math]}$ ∥ $\text{[math]}$ ．

$\text{[math]}$ ▲ （）．

$\text{[math]}$ ，

$\text{[math]}$ ．

$\text{[math]}$ ▲ ∥ ▲ （）．

$\text{[math]}$ ∥ $\text{[math]}$ （）．

取一个自然数，若它是奇数，则乘以3加上1，若它是偶数，则除以2，按此规则经过若干步的计算最终可得到1．这个结论在数学上还没有得到证明．但举例验证都是正确的．例如：取自然数5．最少经过下面5步运算可得1，即： $\text{[math]}$ ，如果自然数 $\text{[math]}$ 最少经过7步运算可得到1，则所有符合条件的 $\text{[math]}$ 的值为．

如图，等边三角形 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 的中点， $\text{[math]}$ 平分 $\text{[math]}$ ，且交 $\text{[math]}$ 于 $\text{[math]}$ .如果用“三角形三条角平分线必交于一点”来证明 $\text{[math]}$ 也一定平分 $\text{[math]}$ ，那么必须先要证明．

完成下面的证明：

在数学活动课上，老师说有人根据如下的证明过程，得到“1＝2”的结论．

设a、b为正数，且a＝b．

∵a＝b，

∴ab＝b² ． ①

∴ab﹣a²＝b²﹣a² ． ②

∴a（b﹣a）＝（b+a）（b﹣a）． ③

∴a＝b+a． ④

∴a＝2a． ⑤

∴1＝2． ⑥

大家经过认真讨论，发现上述证明过程中从某一步开始出现不正确，这一步是（填入编号），造成不正确原因是．

解答题

如图所示，∠B＝∠C，AB∥CD，证明：CE∥BF.

已知：如图， $\text{[math]}$ ， $\text{[math]}$ .

求证： $\text{[math]}$ ∥ $\text{[math]}$ .

如图， $\text{[math]}$ ，点 $\text{[math]}$ 为直线 $\text{[math]}$ ， $\text{[math]}$ 的交点， $\text{[math]}$ .

求证： $\text{[math]}$ .

如图，已知 $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点E， $\text{[math]}$ .

已知：如图，CD⊥AB，FG⊥AB，垂足分别为D、G，点E在AC上，且∠1＝∠2.

如图，已知直线AB∥CD，直线MN分别交AB、CD于M、N两点，若ME、NF分别是∠AMN、∠DNM的角平分线，试说明：ME∥NF

解：∵AB∥CD，（▲ ）

∴∠AMN＝∠DNM（▲）

∵ME、NF分别是∠AMN、∠DNM的角平分线，（已知）

∴∠EMN＝▲∠AMN，

∠FNM＝▲∠DNM（角平分线的定义）

∴∠EMN＝∠FNM（等量代换）

∴ME∥NF（▲）

由此我们可以得出一个结论：两条平行线被第三条直线所截，一对▲角的平分线互相▲．

证明填空：如图，已知直线 $\text{[math]}$ ， $\text{[math]}$ ，

求证： $\text{[math]}$ .

证明： $\text{[math]}$ 已知 $\text{[math]}$

$\text{[math]}$ _▲_ $\text{[math]}$

又 $\text{[math]}$ _▲_ $\text{[math]}$

$\text{[math]}$ _▲_ $\text{[math]}$

$\text{[math]}$ _▲ $\text{[math]}$

$\text{[math]}$ _▲ $\text{[math]}$

如图，AB∥DG，∠1+∠2＝180°，

试卷列表

教育网站链接

在线组卷课件下载评课网课件工坊 PPT模板排课软件云字帖