单选题
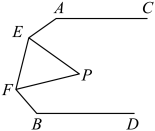
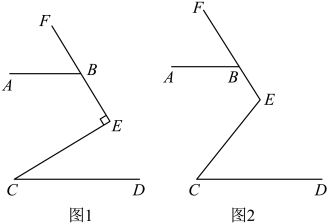
如图,点D为 的角平分线AE延长线上的一点,过点D作
的角平分线AE延长线上的一点,过点D作 于点F,若
于点F,若 ,
,  , 则
, 则 的度数是( )
的度数是( )

- A、
- B、
- C、
- D、
如图,将一副三角板的直角顶点重合,且使 , 则
, 则 的度数是( )
的度数是( )
- A、
- B、
- C、
- D、
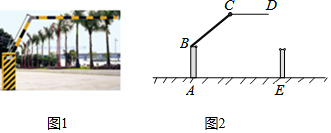
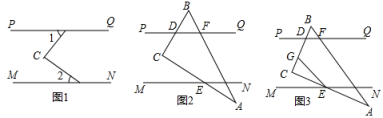
如图所示, ,
,  , 若
, 若 , 则
, 则 的度数为( )
的度数为( )

- A、 100°
- B、 110°
- C、 120°
- D、 130°
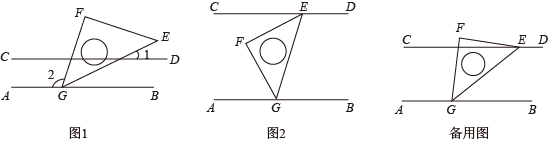
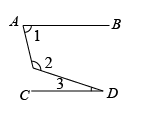
如图,若 ,
,  ,
,  , 则
, 则 的度数是( )
的度数是( )
- A、 25°
- B、 30°
- C、 36°
- D、 38°
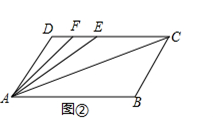
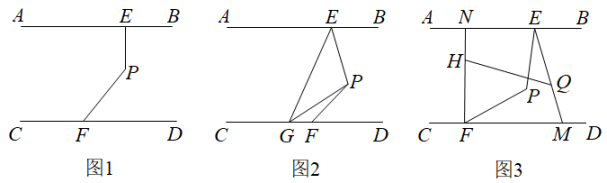
把长方形纸片MNPQ沿AC,AB折叠成如图所示,AM的对应线段 落在AC上,若∠NAC=38°,则
落在AC上,若∠NAC=38°,则 的度数为( )
的度数为( )

- A、 109°
- B、 110°
- C、 115°
- D、 100°
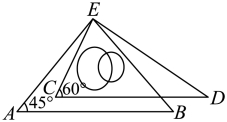
如图, ABC的角平分线CD,BE相交于点F,∠BAC=∠AGB,AG
ABC的角平分线CD,BE相交于点F,∠BAC=∠AGB,AG BC,下列结论中不一定成立的是( )
BC,下列结论中不一定成立的是( )

- A、 ∠BAG=2∠CBE
- B、
- C、 ∠AEB=∠GBE
- D、 ∠ADC=∠AEB