单选题
3的算术平方根是( )
- A、 9
- B、 -9
- C、
- D、
- A、 0
- B、
- C、
- D、
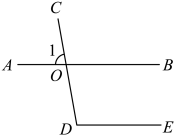
如图,直线 、
、 相交于点
相交于点 , ∠1=80°,如果
, ∠1=80°,如果 ∥
∥ , 那么
, 那么 的度数是( )
的度数是( )
- A、 80°
- B、 90°
- C、 100°
- D、 110°
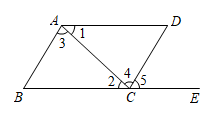
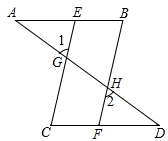
如图,下列说法错误的是( )

- A、
与
是同位角
- B、
与
是内错角
- C、
与
是对顶角
- D、
与
是同旁内角
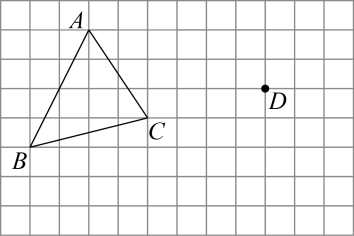
如图,∠ACB=90°,将直角三角形ABC沿着射线BC方向平移5cm,得三角形 , 已知BC=3cm,AC=4cm,AB=5cm,则阴影部分(四边形
, 已知BC=3cm,AC=4cm,AB=5cm,则阴影部分(四边形 )的周长为( )
)的周长为( )

- A、 16cm
- B、 18cm
- C、 20cm
- D、 22cm