选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个.
下列四个品牌图标中,是中心对称图形的是( )
- A、

- B、

- C、

- D、
用配方法解一元二次方程x2-8x+3=0,此方程可化为( )
- A、 (x-4)2=13
- B、 (x+4)2=13
- C、 (x-4)2=19
- D、 (x+4)2=19
如图中的五角星图案,绕着它的中心O旋转n°后,能与自身重合,则n的值至少是( )

- A、 60
- B、 72
- C、 120
- D、 144
在平面直角坐标系xOy中,将抛物线y=2x2先向左平移2个单位,再向下平移3个单位,所得抛物线为( )
- A、 y=2(x-2)2+3
- B、 y=2(x-2)2-3
- C、 y=2(x+2)2-3
- D、 y=2(x+2)2+3
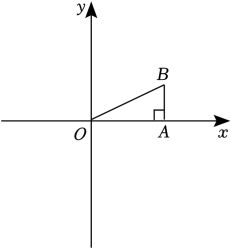
在平面直角坐标系xOy中,一次函数y=ax2+bx+c(a≠0)的图象如图所示示,关于a、c的符号判断正确的是( )
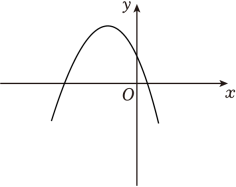
- A、 a>0,c>0
- B、 a>0,c<0
- C、 a<0,c>0
- D、 a<0,c<0
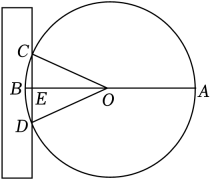
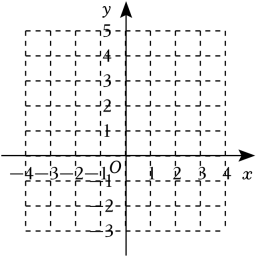
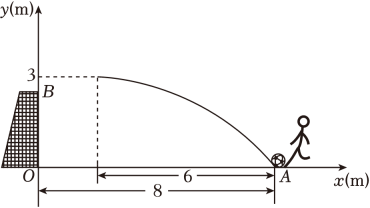
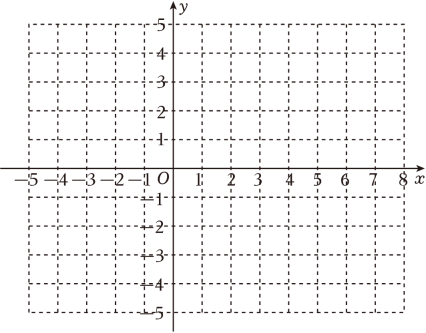
雷达通过无线电的方法发现目标并测定它们的空间位置,因此雷达被称为“无线电定位”.现有一款监测半径为5km的雷达,监测点的分布情况如图,如果将雷达装置设在P点,每一个小格的边长为1km , 那么能被雷达监测到的最远点为( )
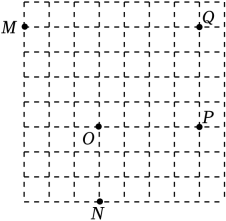
- A、 M点
- B、 N点
- C、 P点
- D、 Q点
二次函数y=ax2+bx+c(a≠0)的图象是抛物线G , 自变量x与函数y的部分对应值如下表:
x | … | -3 | -2 | -1 | 0 | 1 | 2 | … |
y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
下列说法错误的是( )
- A、 抛物线G的开口向上
- B、 抛物线G的对称轴是
- C、 抛物线G与y轴的交点坐标为(0,-2)
- D、 二次函数y=ax2+bx+c(a≠0)的最小值为-2
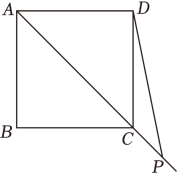
两块完全相同的含30°角的直角三角板ABC和A'B'C′重合在一起,将三角板A'B'C'绕直角顶点C'按逆时针方向旋转α(0°<α≤90°),如图所示.以下结论错误的是( )
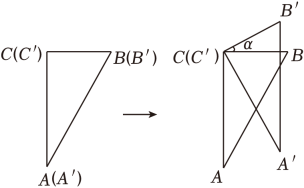
- A、 当α=30°时,A'C与AB的交点恰好为AB中点
- B、 当α=60°时,A'B'恰好经过点B
- C、 在旋转过程中,存在某一时刻,使得AA'=BB'
- D、 在旋转过程中,始终存在AA'⊥BB'