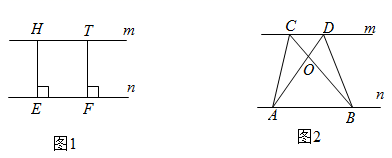选择题
小红在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线ln(n=1,2,3,4,5,6,7),其中l1、l2互相平行,l3、l4、I5三条直线交于一点,则他探究这7条直线的交点个数最多是( )
- A、 17个
- B、 18个
- C、 19个
- D、 21个
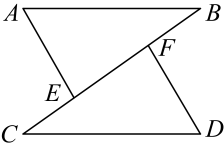
在探究“过直线外一点P作已知直线a的平行线”的活动中,王玲同学通过如下的折纸方式找到了符合要求的直线,在这个过程中她可能用到的推理依据组合是( )

①平角的定义;②邻补角的定义;③角平分线的定义;④同旁内角互补,两直线平行;⑤两直线平行,内错角相等.
- A、 ②④
- B、 ③⑤
- C、 ①②⑤
- D、 ①③④
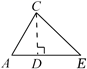
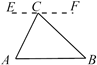
在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )
- A、 过C作EF
AB
- B、 过AB上一点D作DE
BC,DF
AC
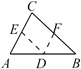
- C、 延长AC到F,过C作CE
AB

- D、 作CD⊥AB于点D