选择题
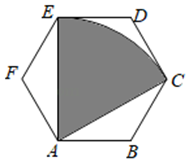
如图,▱ 中,
中, ,
,  , 以
, 以 为直径的
为直径的 交
交 于点
于点 , 则
, 则 的长为( )
的长为( )

- A、
- B、
- C、
- D、
如图,在 中,直径
中,直径 , 点D为AB上方圆上的一点,
, 点D为AB上方圆上的一点, ,
,  于点E , 点P是OE上一点,连接DP , AP , 得出下列结论:
于点E , 点P是OE上一点,连接DP , AP , 得出下列结论:
Ⅰ:阴影部分的面积随着点P的位置的改变而改变,其最小值为 .
Ⅱ:阴影部分的周长随着点P的位置的改变而改变,其最小值为 .

下列判断正确的是( ).
- A、 只有Ⅰ正确
- B、 只有Ⅱ正确
- C、 Ⅰ、Ⅱ都正确
- D、 Ⅰ、Ⅱ都不正确