选择题
下列四个数中,其倒数是正整数的数是( )
- A、 2
- B、 ﹣2
- C、
- D、 ﹣
下列美丽的图案,是轴对称图形但不是中心对称图形的是( )
- A、

- B、

- C、

- D、

在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 1 | 3 | 0 | 2 | 3 | 4 | 2 | 1 | 1 | 3 |
根据以上数据,估算袋中的白棋子数量为( )
- A、 60枚
- B、 50枚
- C、 40枚
- D、 30枚
在显微镜下,一种细菌的形状可以近似地看成圆,它的半径约为0.00000063m,这个数据用科学记数法表示为( )
- A、 0.63×10﹣6m
- B、 6.3×10﹣7m
- C、 6.3×10﹣8m
- D、 63×10﹣8m
如图,▱ABCD中,AB=4,BC=5,∠ABC=60°,对角线AC,BD交于点O,过点O作OE⊥AD,则OE等于( )

- A、
- B、 2
- C、 2
- D、 2.5
如图,AB是⊙O的直径,AC与⊙O相切于点A,连接OC交⊙O于D,作DE∥AB交⊙O于E,连接AE,若∠C=40°,则∠E等于( )

- A、 40°
- B、 50°
- C、 20°
- D、 25°
点P是图①中三角形上一点,坐标为(a,b),图①经过变化形成图②,则点P在图②中的对应点P′的坐标为( )
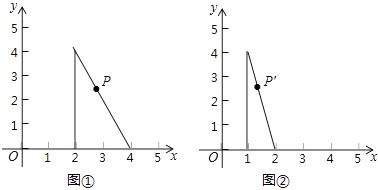
- A、 (
a,b)
- B、 (a﹣1,b)
- C、 (a﹣2,b)
- D、 (
a,
b)













