单选题
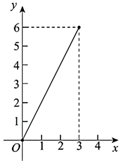
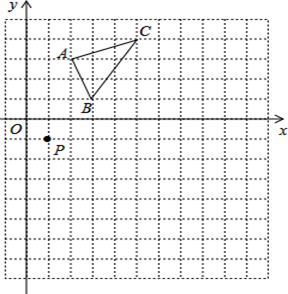
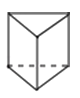
一个几何体的三视图如图所示,则这个几何体是( )
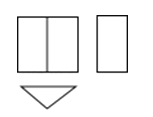
- A、
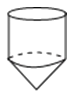
- B、
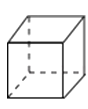
- C、
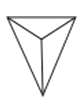
- D、
2019年10月1日,庆祝中华人民共和国成立70周年大会在北京天安门广场隆重举行.10月3日微博观看互动量累计达到19280000次,将19280000用科学记数法表示为( )
- A、 1.928 × 104
- B、 1928×104
- C、 1.928 × 107
- D、 0.1928 × 108
某班七个兴趣小组人数如下:5,6,6,x,7,8,9,已知这组数据的平均数是7,则这组数据的中位数是( )
- A、 6
- B、 6.5
- C、 7
- D、 8
某工厂第二季度的产值比第一季度的产值增长了x%,第三季度的产值又比第二季度的产值增长了x%,则第三季度的产值比第一季度的产值增长了( )
- A、 2x%
- B、 1+2x%
- C、 (1+x%)x%
- D、 (2+x%)x%
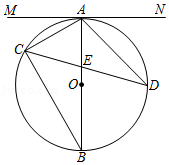
如图,⊙O是正五边形ABCDE的外接圆,点P是  的一点,则∠CPD的度数是( )
的一点,则∠CPD的度数是( )
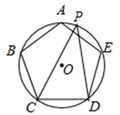
- A、 30°
- B、 36°
- C、 45°
- D、 72°