单选题
剪纸是我国传统民间艺术,下列“花朵”剪纸作品中,是中心对称图形的是( )
- A、

- B、

- C、

- D、

一元二次方程x2+x=0的根的是( )
- A、 x1=0,x2=1
- B、 x1=0,x2=﹣1
- C、 x1=1,x2=﹣1
- D、 x1=x2=﹣1
用配方法将x2﹣8x﹣1=0变形为(x﹣4)2=m,下列选项中,m的值是正确的是( )
- A、 17
- B、 15
- C、 9
- D、 7
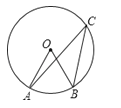
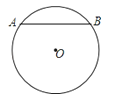
如图,⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,则⊙O的半径长为( )
- A、 3cm
- B、 4cm
- C、 5cm
- D、 6cm
将抛物线y=(x﹣1)2向右平移1个单位后所得到抛物线的解析式是( )
- A、 y=(x﹣2)2
- B、 y=x2
- C、 y=x2+1
- D、 y=x2﹣1
在下列事件中,随机事件是( )
- A、 通常温度降到0℃以下,纯净的水会结冰
- B、 随意翻到一本书的某页,这页的页码是奇数
- C、 明天的太阳从东方升起
- D、 在一个不透明的袋子里装有完全相同的6个红色小球,随机抽取一个白球
若抛物线y=ax2+bx+c与x轴的两个交点坐标是(﹣1,0)和(3,0),则抛物线的对称轴是( )
- A、 x=﹣1
- B、 x=﹣
- C、 x=
- D、 x=1
圆心角为120°,弧长为12π的扇形半径为( )
- A、 6
- B、 9
- C、 18
- D、 36