单选题
一元二次方程  化为一般式后的二次项、一次项、常数项分别是( )
化为一般式后的二次项、一次项、常数项分别是( )
- A、
,8x,2
- B、
,
,
- C、
,
,
- D、
,
,2
若一元二次方程  的两个根为m,n,则一次函数
的两个根为m,n,则一次函数  的图象是( )
的图象是( )
- A、

- B、

- C、

- D、

在Rt△ABC中,AB=6,BC=8,则这个三角形的内切圆的半径是( )
- A、 5
- B、 2
- C、 5或2
- D、 2或
-1
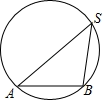
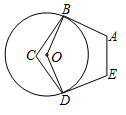
如图,点  在圆上,若弦
在圆上,若弦  的长度等于圆半径的
的长度等于圆半径的  倍,则
倍,则  的度数是( ).
的度数是( ).
- A、 22.5°
- B、 30°
- C、 45°
- D、 60°
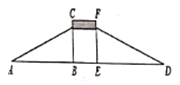
如图,为方便行人推车过天桥,市政府在10m高的天桥两端分别修建了50m长的斜道.用科学计算器计算这条斜道的倾斜角,下列按键顺序正确的是( )
- A、 sin0.2=
- B、 2ndFsin0.2=
- C、 tan0.2=
- D、 2ndFtan0.2=
如图,△ABC的顶点都是正方形网格中的格点,则cos∠ACB等于( )

- A、
- B、
- C、
- D、
为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如图所示(单位:cm),则该铁球的直径为( )

- A、 12cm
- B、 10cm
- C、 8cm
- D、 6cm
如图,在  中,
中,  ,
,  于点D,
于点D,  ,
,  ,则线段 AC的长为( )
,则线段 AC的长为( )

- A、 10
- B、 8
- C、
- D、
如图,⊙O与正五边形ABCDE的边AB,DE分别相切于点B,D,则劣弧BD所对的圆心角∠BOD的大小为( )
- A、 108°
- B、 118°
- C、 144°
- D、 120°